NEW: Đề thi vào 10 môn Toán 2021 Lâm Đồng
Đề thi tuyển sinh vào lớp 10 môn Toán chuyên năm 2020 Lâm Đồng và đáp án được ĐọcTàiLiệu cập nhật giúp các em học sinh tham khảo, so sánh kết quả với bài thi của mình.
Đề thi vào lớp 10 năm 2020
Chi tiết đề thi vào lớp 10 môn Toán chuyên của tỉnh Lâm Đồng như sau:
|
Sở GD&ĐT Lâm Đồng ĐỀ CHÍNH THỨC |
KỲ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC: 2020 - 2021 Môn: Toán (chuyên) |

Đáp án đề tuyển sinh vào lớp 10 môn Toán chuyên Lâm Đồng 2020
Câu 1:
Ta có:
\(-m^2 + 2m - 10 = - (m-1)^2 - 9 \leq -9 < 0\) với mọi m
hay hàm số đã cho luôn nghịch biến (đpcm).
Câu 2:
\(\sqrt{4-x^2} + 6 = 2\sqrt{2+x} + 3\sqrt {2-x}\)
ĐKXĐ: \(-2 \leq x \leq 2\)
\(\Leftrightarrow \sqrt{(2+x)(2-x)} + 6 = 2\sqrt{2+x} + 3\sqrt {2-x}\)
\(\Leftrightarrow ( \sqrt{2+x} -3)(\sqrt {2-x} - 2) = 0\)
\(\Leftrightarrow \left[ \matrix{ \sqrt{2+x}=3 \hfill \cr \sqrt{2-x}=2 \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ x =7 & (loại) \hfill \cr x =-2 & (tm) \hfill \cr} \right.\)
KL....
Câu 3:
Đặt \(n^2 + 18n + 2020 = a^2 \) (a ∈ ℕ*)
\(⇔ (n+9)^2 + 1939 = a^2 \)
\(⇔ 1.1939 = 7.277 = a^2 - (n+9)^2 = (a-n-9)(a+n+9)\)
Dễ thấy a + n + 9 > a - n - 9
\(⇒ \left[ \matrix{ \left\{ \matrix{ a-n-9 = 1 \hfill \cr a+n+9 = 1939 \hfill \cr} \right. \hfill \cr \left\{ \matrix{ a-n-9 = 7 \hfill \cr a+n+9 = 277 \hfill \cr} \right. \hfill \cr} \right.\)
\(⇔ \left[ \matrix{ \left\{ \matrix{ a = 970 \hfill \cr n+9 = 969 ⇔ n = 960 \hfill \cr} \right. \hfill \cr \left\{ \matrix{ a = 142 \hfill \cr n+9 = 135 ⇔ n = 126 \hfill \cr} \right. \hfill \cr} \right.\) (tm)
KL....
Câu 4:
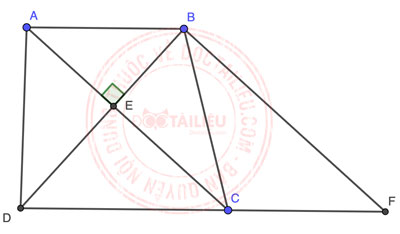
Gọi BD cắt AC tại E. Vẽ đường thẳng BF // AC, F thuộc CD.
Gọi h (cm) là đường cao cần tìm.
Xét tứ giác ABFC có AB // CF, AC // BF ⇒ ABFC là hình bình hành ⇒ AB = CF và AC = BF = 8 cm.
Vì BD ⊥ AC, và BF // AC ⇒ BF ⊥ BD, áp dụng định lý Pytago ta có:
\(⇒ AB + CD = CF + CD = DF = \sqrt{{BD}^2 + {BF}^2} = \sqrt{{6}^2 + {8}^2} = 10\) (cm)
Ta có:
\(2S_{\triangle DBF} = BD.BF = h.DF\)
\(⇒ h = \dfrac{BD.BF}{DF} = \dfrac{6.8}{10} = 4,8\)
(cm)KL...
Câu 5:
\(a^2 + b^2 + c^2 + d^2 + e^2 \geq a(b+c+d+e)\)
\(⇔ 4a^2 + 4b^2 + 4c^2 + 4d^2 + 4e^2 \geq 4a(b+c+d+e)\)
\(⇔ (a^2 - 4ab + 4b^2) + (a^2 - 4ac + 4c^2) + (a^2 - 4ad + 4d^2) +(a^2 - 4ae+ 4e^2) \geq 0\)
\(⇔ (a-2b)^2 + (a-2c)^2 + (a-2d)^2 + (a-2e)^2 \geq 0\)
BĐT cuối luôn đúng, mà các phép biến đổi là tương đương nên ta có đpcm.
Dấu bằng xảy ra ⇔ a = 2b = 2c = 2d = 2e.
Câu 6:
Để PT đã cho có hai nghiệm phân biệt ⇔
\(\Delta = m^2 - 4n = m^2 - 4(4-m) = m^2 + 4m - 16 > 0 \)
\(⇔ \left[ \matrix{ m > - 2 + 2 \sqrt 5 \hfill \cr m < - 2 - 2 \sqrt 5 \hfill \cr} \right.\)
Vì x₁, x₂ là nghiệm của phương trình đã cho nên:
\(x_2^2 + mx_2 + n = 0 ⇔ x_2^2 = -mx_2 -n = -mx_2 - 4 + m\)
Vì:
\(x_1- x_2 = x_2^2 \geq 0 ⇒ x_1 \geq x_2\)
\(⇒ \left\{ \matrix{ x_1 = \dfrac{-m +\sqrt{\Delta}}2 \hfill \cr x_2 = \dfrac{-m -\sqrt{\Delta}}2 \hfill \cr} \right. \)
Thay vào ta có:
\(x_1 = x_2 + x_2^2 = x_2 - mx_2 -4+m\)
\(⇔ \dfrac{-m +\sqrt{\Delta}}2 = \dfrac{-m-\sqrt{\Delta}}2. (1 - m) -4 + m\)
\(⇔ -m +\sqrt{\Delta} = (-m-\sqrt{\Delta}) (1 - m) -8 + 2m\)
\(⇔ -m +\sqrt{\Delta} = -m-\sqrt{\Delta} + m^2 + m\sqrt{\Delta} -8 + 2m\)
\(⇔ \sqrt{\Delta} (2-m) = m^2 + 2m - 8 = (m-2)(m+4)\)
\(⇔ \left[ \matrix{ m = 2 & (loại)\hfill \cr \sqrt {\Delta} = -m - 4 \hfill \cr} \right.\)
⇒ \(\left\{ \matrix{ -m - 4 \geq 0 ⇔ m \leq -4 \hfill \cr \Delta = (-m-4)^2 ⇔ m^2 + 4m - 16 = m^2+ 8m + 16 \hfill \cr} \right.\)
\(⇔ \left\{ \matrix{ m < -2-2\sqrt 5 \hfill \cr 4m = 32 ⇔ m = 8 &(loại) \hfill \cr} \right.\)
KL Vô nghiệm.
Câu 7:
Gọi số quyển vở tổ chức đó có là A (A ∈ ℕ*)
Gọi số vở ở mỗi phần quà ban đầu là B (B ∈ ℕ*)
Ta có số phần quà ban đầu là: \(\dfrac{A}{B}\)
Theo bài ra ta có hệ:
\(\left\{ \matrix{ \dfrac{A}{B-6} = \dfrac{A}{B} + 5 \hfill \cr \dfrac{A}{B-10} = \dfrac{A}{B} + 10 \hfill \cr} \right.\)
\(⇔ \left\{ \matrix{ AB =A(B-6)+ 5B(B-6) \hfill \cr AB =A(B-10)+ 10B(B-10) \hfill \cr} \right.\)
\(⇔ \left\{ \matrix{ 6A = 5B^2 - 30 B = 6B^2 - 60B \hfill \cr A = B^2 - 10B \hfill \cr} \right.\)
\(⇔ \left\{ \matrix{ B^2 -30B = 0 \hfill \cr A = B^2 - 10B \hfill \cr} \right.\)
\(⇔ \left\{ \matrix{ \left[ \matrix{ B = 0 &(Loại) \hfill \cr B = 30 &(tm) \hfill \cr} \right. \hfill \cr A = B^2 - 10B \hfill \cr} \right.\)
⇒ A = 600 (quyển vở).
KL...
Câu 8:
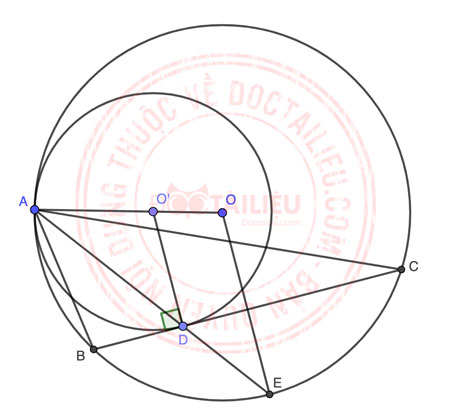
Kéo dài AD cắt (O;R) tại điểm thứ hai là E.
Ta thấy △O'AD cân tại O' (do O'A = O'D = R') ⇒ ∠O'AD = ∠O'DA.
Tương tự, △OAE có OA = OE = R ⇒ △OAE cân tại O ⇒ ∠OEA = ∠OAE = ∠O'AD = ∠O'DA
⇒ O'D // OE (góc ở vị trí đồng vị bằng nhau)
Mà O'D ⊥ BC (do BC là tiếp tuyến của (O';R') ⇒ OE ⊥ BC ⇒ E là điểm chính giữa cung BC
⇒ AE là phân giác góc BAC, hay AD là phân giác của góc BAC (đpcm).
Câu 9:
Vì x; y; z đôi một khác nhau và thoả mãn đề bài, nên x; y; z là 3 nghiệm phân biệt của phương trình
\(X^3-3X + 1 = 0\)
và \((X-x)(X-y)(X-z) = 0\)
\(\Leftrightarrow X^3 - X^2 (x+y+z) + X (xy+yz+zx) - xyz = 0\)
\( ⇒\left\{ \matrix{ x+y+z = 0 \hfill \cr xy+yz+zx = -3 \hfill \cr xyz = -1 \hfill \cr} \right. \)
Ta có:
\(S = x^2 + y^2 + z^2 = (x+y+z)^2 - 2(xy + yz + zx) \)
\( = 0^2 - 2.(-3) = 6\)
Câu 10:
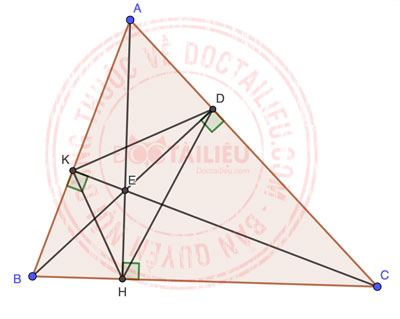
Ta thấy ∠BKE = ∠BHE = 90° ⇒ tứ giác BKEH nội tiếp ⇒ ∠BHK = ∠BEK.
Tương tự, tứ giác AKED nội tiếp ⇒ ∠KAD = 180° - ∠KED = ∠BEK
⇒ ∠BHK = ∠KAD = ∠BAC.
Tương tự, tứ giác HEDC nội tiếp ⇒ ∠CHD = ∠CED = ∠BEK = ∠BAC
⇒ ∠KHD = 180° - ∠BHK - ∠CHD = 180° - 2.∠BAC = 180° - 2.∠A
Áp dụng công thức sin, ta có:
\(\dfrac{S_{HDK}}{S_{ABC}} = \dfrac{HK.HD.sin(180° - 2A)}{AB.AC.sinA} = \dfrac{HK.HD.sin2A}{AB.AC.sinA} = \dfrac{2.HK.HD.cosA}{AB.AC} \)
Xét △BKH và △BCA có:
Góc ∠ABC chung
∠BKH = ∠BEH = 180° - ∠HED = ∠BCA
Suy ra △BKH ∽ △BCA ⇒ \(\dfrac{HK}{AC} = \dfrac{BK}{BC} = \dfrac{BH}{AB} \)
Tương tự, chứng minh được △CHD ∽ △CAB ⇒ \(\dfrac{HD}{AB} = \dfrac{CH}{CA} = \dfrac{CD}{CB} \).
Ta lại có:
\(cos A = \dfrac{AD}{AB} = \dfrac{AK}{AC} \)
\(cos B = \dfrac{BK}{BC} = \dfrac{BH}{BA} \)
\(cos C = \dfrac{CH}{CA} = \dfrac{CD}{CB} \)
Ta có:
\(\dfrac{S_{HDK}}{S_{ABC}} = \dfrac{2.HK.HD.cosA}{AB.AC} = 2.\dfrac{BK}{BC}.\dfrac{CD}{BC}.cos A = 2cosB.cosC.cosA \)
\(= 2cosB.cosC.cos(\pi -B-C) = -2cosB.cosC.cos(B+C)\)
Thay vào, ta có:
\(\dfrac{S_{HDK}}{S_{ABC}} + {cos}^2 A + {cos}^2 B + {cos}^2 C = -2cosB.cosC.cos(B+C) + {cos}^2 (B+C) + {cos}^2 B + {cos}^2 C\)
\(= -2cosB.cosC.(cosB.cosC - sinB.sinC)+ (cosB.cosC - sinB.sinC)^2 + {cos}^2 B + {cos}^2 C\)
\(=(cosB.cosC - sinB.sinC) (cosB.cosC - sinB.sinC -2cosB.cosC) + {cos}^2 B + {cos}^2 C\)
\(=-(cosB.cosC - sinB.sinC) (cosB.cosC + sinB.sinC) + {cos}^2 B + {cos}^2 C\)
\(=-{cos}^2B.{cos}^2C + {sin}^2B.{sin}^2C + {cos}^2 B + {cos}^2 C\)
\(=-{cos}^2B.{cos}^2C + (1-{cos}^2B).(1-{cos}^2C) + {cos}^2 B + {cos}^2 C\)
\(=1\)
Hay \(\dfrac{S_{HDK}}{S_{ABC}} + {cos}^2 A + {cos}^2 B + {cos}^2 C = 1\) (đpcm).
-/-
Các môn thi khác
• Đề thi tuyển sinh vào lớp 10 môn Văn năm 2020 Lâm Đồng
Trên đây là toàn bộ nội dung của đáp án đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 của tỉnh Lâm Đồng được Đọc Tài Liệu thực hiện sau khi kì thi chính thức diễn ra. Với nội dung này các em có thể so sánh đối chiếu kết quả bài thi của mình!
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành hữu ích với bạn trong kỳ thi này.
