Đáp án đề thi vào lớp 10 môn Toán năm 2020 Chuyên KHTN (vòng 1)

    Đề thi tuyển sinh vào lớp 10 môn Toán (vòng 1) năm 2020 Chuyên KHTN và đáp án được Đọc Tài Liệu cập nhật giúp các em học sinh tham khảo, so sánh kết quả với bài thi của mình.

Đề thi vào lớp 10 năm 2020

Chi tiết đề thi vào lớp môn Toán của Chuyên KHTN như sau:

Trường THPT Chuyên KHTN ĐỀ CHÍNH THỨC

KỲ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC: 2020 - 2021 Môn: Toán

Đáp án đề tuyển sinh vào lớp 10 môn Toán Chuyên KHTN 2020

Câu 1:

1)

\(\left\{ \matrix{ x^2+y^2 + xy = 7 &(1) \hfill \cr 9x^3 = xy^2 + 70(x-y) &(2) \hfill \cr} \right. \)

Ta có:

(2) \(\Leftrightarrow 9x^3 = xy^2 + 10(x-y).7\)

\(\Leftrightarrow 9x^3 = xy^2 + 10(x-y)(x^2+y^2+xy) \)

\(\Leftrightarrow 9x^3 = xy^2 + 10(x^3-y^3) \)

\(\Leftrightarrow xy^2 + x^3- 10y^3 = 0\)

\(\Leftrightarrow (x-2y)(x^2 + 2xy + 5y^2) = 0\)

\(\Leftrightarrow \left[ \matrix{ x= 2y \hfill \cr x^2 + 2xy + 5y^2 =0 \hfill \cr} \right.\)

\(\Leftrightarrow \left[ \matrix{ x= 2y \hfill \cr (x+y)^2+ 4y^2 =0 \hfill \cr} \right.\)

\(\Leftrightarrow \left[ \matrix{ x= 2y \hfill \cr (x+y)^2 = 4y^2 = 0 \Leftrightarrow x= y = 0 &(loại) \hfill \cr} \right.\)

Thay x = 2y vào (1), ta có hệ:

\(\Leftrightarrow \left\{ \matrix{ x = 2y \hfill \cr 4y^2+y^2 + 2y^2 = 7 \hfill \cr} \right. \)

\(\Leftrightarrow \left\{ \matrix{ x = 2y \hfill \cr 7y^2 = 7 \Leftrightarrow y = ±1 \hfill \cr} \right. \)

\(\Leftrightarrow \left[ \matrix{ (x;y) = (2;1) \hfill \cr (x;y) = (-2;-1) \hfill \cr} \right. \)

KL....

2) 

\(11 \sqrt {5-x} + 8\sqrt{2x-1} = 24 + 3 \sqrt{(5-x)(2x-1)}\)  (1)

(ĐKXĐ: \(\dfrac{1}2 \leq x \leq 5\))

Đặt: \(\sqrt {5-x} = a\)

\(\sqrt {2x - 1} = b\) (\(a;b \geq 0\))

\(\Rightarrow 5 - a^2 = x = \dfrac{b^2+1}2\)

\(\Leftrightarrow 2a^2 = 9 - b^2\)

\(\Leftrightarrow 2a^2 = (3-b)(3+b)\)

Ta có:

(1) \(\Leftrightarrow 11 a + 8b = 24 + 3ab\)

\(\Leftrightarrow 2a= 8(3- b) - 3a(3-b) = (8-3a)(3-b)\)

\(\Rightarrow 2a^2 = (8-3a)(3-b)a\)

\(\Leftrightarrow (3-b)(3+b) = (8-3a)(3-b)a\)  (*)

Với b = 3 ⇔ x = 5 (thỏa mãn)

Với b ≠ 3 ⇔

\(3+b= (8-3a)a = -3a^2 + 8a\)

\(\Leftrightarrow 3 + b + a^2 = -2a^2+ 8a\)

\(\Leftrightarrow 3 + b +\dfrac{ 9-b^2}2 = -2a^2+ 8a\)

\(\Leftrightarrow b^2 - 2b +1= 4a^2 - 16a + 16\)

\(\Leftrightarrow (b-1)^2= (2a-4)^2\)

\(\Leftrightarrow \left[ \matrix{ b-1= 2a-4 & (2) \hfill \cr b-1= 4-2a & (3) \hfill \cr} \right. \)

Ta có:

(2) \(\Leftrightarrow \sqrt {2x - 1}-1= 2\sqrt{5-x}-4\)

\(\Leftrightarrow \sqrt {2x - 1}= 2\sqrt{5-x}-3\)

\(\Leftrightarrow \left\{ \matrix{ 2x-1= 4(5-x)+9 - 12\sqrt{5-x} \hfill \cr 2\sqrt{5-x} - 3 \geq 0 \hfill \cr} \right. \)

\(\Leftrightarrow \left\{ \matrix{ 6(5-x)- 12\sqrt{5-x} =0 \hfill \cr 5-x \geq \dfrac{9}4 \hfill \cr} \right. \)

\(\Leftrightarrow \left\{ \matrix{ \left[ \matrix{ \sqrt{5-x} = 0\hfill \cr \sqrt{5-x} = 2 \hfill \cr} \right. \hfill \cr x \leq \dfrac{11}4 \hfill \cr} \right. \)

\(\Leftrightarrow \left\{ \matrix{ \left[ \matrix{ x = 5 &(tm)\hfill \cr x= 1 &(tm)\hfill \cr} \right. \hfill \cr x \leq \dfrac{11}4 \hfill \cr} \right. \)

(3) \(\Leftrightarrow \sqrt {2x - 1}-1= 4-2\sqrt{5-x}\)

\(\Leftrightarrow \sqrt {2x - 1}=5 -2\sqrt{5-x}\)

\(\Leftrightarrow \left\{ \matrix{ 2x-1= 4(5-x)+25 - 20\sqrt{5-x} \hfill \cr 5-2\sqrt{5-x} \geq 0 \hfill \cr} \right. \)

\(\Leftrightarrow \left\{ \matrix{ 6(5-x)- 12\sqrt{5-x} +16 =0 \hfill \cr 5-x \leq \dfrac{25}4 \hfill \cr} \right. \)

Dễ thấy vô nghiệm.

KL: PT có 2 nghiệm x = 5 hoặc x = 1.

Câu 2:

1)

\(x^2y^2 - 16xy + 99 = 9x^2 + 36y^2 + 13x + 26y\)

\(\Leftrightarrow x^2y^2 + 20xy + 99 = 9x^2 + 36y^2+ 36xy + 13x + 26y\)

\(\Leftrightarrow (xy+ 10)^2 - 1 = 9(x+2y)^2 + 13(x+2y)\)

\(\Leftrightarrow (xy+ 10)^2 = 9(x+2y)^2 + 13(x+2y) + 1\)

là số chính phương. Với mọi x, y nguyên dương, ta có:

\(9(x+2y)^2 + 6(x+2y) + 1 < 9(x+2y)^2 + 13(x+2y) + 1 < 9(x+2y)^2 + 18(x+2y) + 9\)

\(\Leftrightarrow (3x+6y+1)^2 < 9(x+2y)^2 + 13(x+2y) + 1 < (3x+6y+3)^2\)

\(\Leftrightarrow 9(x+2y)^2 + 13(x+2y) + 1 = (3x+6y+2)^2\)

\(\Leftrightarrow 9(x+2y)^2 + 13(x+2y) + 1 = 9(x+2y)^2 + 12(x+2y) + 4\)

\(\Leftrightarrow x+2y = 3\)

Mà x,y ∈ ℕ* ⇒ x = y = 1 (thử lại thỏa mãn).

KL....

2)

Ta có:

\(8a + 12b \leq 2a^2 + 3b^2 + 5ab + 10 = (2a+3b)(a+b)+10 \leq 5(a+b) + 10\)

\(\Leftrightarrow 3a + 7b \leq 10\)

Ta cần chứng minh:

\(3a^2 + 8b^2 + 10ab \leq 21\)

\(\Leftrightarrow (a+2b)(3a+4b) \leq 21\)

Ta có:

\(8a+13b = \dfrac{17}5 (2a+3b) + \dfrac{2}5 (3a+7b) \leq \dfrac{17}5 .5+ \dfrac{2}5.10=21\)

Áp dụng BĐT AM-GM ta có:

\(2(8a+13b) = (7a+14b)+ (9a+12b) \geq 2\sqrt{(7a+14b)(9a+12b)}\)

\(\Leftrightarrow2\sqrt{21(a+2b)(3a+4b)} \leq 2(8a+13b) \leq 2.21\)

\(\Leftrightarrow \sqrt{21(a+2b)(3a+4b)} \leq 21\)

\(\Leftrightarrow (a+2b)(3a+4b) \leq 21\) (đpcm).

Dấu bằng xảy ra ⇔ a = b = 1.

Câu 3:

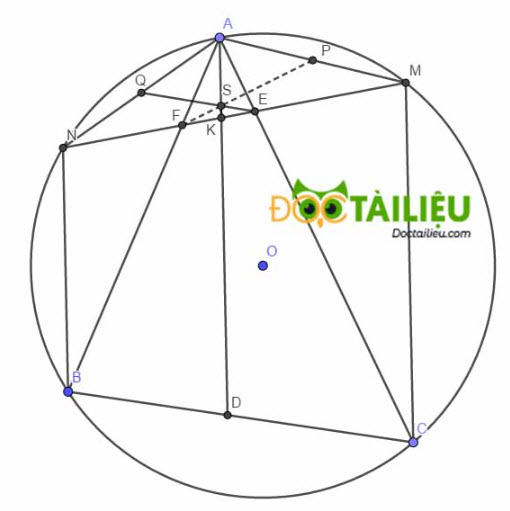
1) 

Ta có: ∠NBA = ∠BAD (sole trong) = ∠DAC (AD là phân giác góc BAC) = ∠ACM (sole trong)

⇒ \(\stackrel\frown{NA} = \stackrel\frown{AM}\) ⇒ AM = AN (đpcm).

2)

Ta có:

\(∠AFE = \dfrac{sd\stackrel\frown{AM} + sd\stackrel\frown{BN}}2 = \dfrac{sd\stackrel\frown{AN} + sd\stackrel\frown{BN}}2 = \dfrac{sd\stackrel\frown{AB}}2 = ∠ACB\)

Hay ∠ECB = ∠ACB = ∠AFE = 180° - ∠BFE ⇒ ∠ECB + ∠EFB = 180°

⇒ Tứ giác EFBC nội tiếp (đpcm).

3)

Gọi EQ cắt AD tại S, AD cắt EF tại K. Theo định lý Menelaus cho tam giác ANK cát tuyến E, S, Q ta có:

\(\dfrac{EN}{EK} . \dfrac{SK}{SA}.1 =1\) ⇒ \(\dfrac{EN}{EK} = \dfrac{SA}{SK}\)  (1)

Gọi FP cắt AD tại S'. Tương tự ta có: \(\dfrac{S'A}{S'K} = \dfrac{FM}{FK}\)  (2)

Theo định lý Thales, ta có:

\(\dfrac{KM}{KN} = \dfrac{DC}{DB} = \dfrac{AC}{AB} = \dfrac{AF}{AE} = \dfrac{KF}{KE} \)

⇒ \(\dfrac{KM}{KN} = \dfrac{KF}{KE} = \dfrac{KM + KF}{KN + KE} = \dfrac{FM}{EN}\)

⇒ \( \dfrac{FM}{FK} = \dfrac{EN}{EK} \)  (3)

Từ (1) (2) và (3) suy ra \( \dfrac{SA}{SK} = \dfrac{S'A}{S'K}\) hay S ≡ S', tức là FP, EQ, AD đồng quy (đpcm).

Câu 4:

\(\dfrac{a(a+bc)^2}{b(ab+2c^2)} + \dfrac{b(b+ca)^2}{c(bc+2a^2)} + \dfrac{c(c+ab)^2}{a(ca+2b^2)} \geq 4\)

Áp dụng BĐT Cauchy - Schwarz, ta có:

\(VT = \dfrac{(a^2+abc)^2}{ab(ab+2c^2)} + \dfrac{(b^2+abc)^2}{bc(bc+2a^2)} + \dfrac{(c^2+abc)^2}{ac(ca+2b^2)} \geq \dfrac{(a^2+b^2+c^2+3abc)^2}{a^2b^2+b^2c^2+c^2a^2 + 2abc(a+b+c)}\)

\(\Leftrightarrow VT \geq \dfrac{(a^2+b^2+c^2+3abc)^2}{(ab+bc+ca)^2}\)

Ta đi chứng minh:

\(\dfrac{(a^2+b^2+c^2+3abc)^2}{(ab+bc+ca)^2} \geq 4\)  (*)

\(\Leftrightarrow \dfrac{a^2+b^2+c^2+3abc}{ab+bc+ca} \geq 2\)

\(\Leftrightarrow a^2+b^2+c^2+3abc \geq 2(ab+bc+ca)\)

Theo nguyên lý Dirichlet, trong 3 số a-1; b-1; c-1 luôn có 2 số cùng dấu.

Không mất tính tổng quát ta giả sử 2 số đó là a-1 và b-1

⇒ \((a-1)(b-1) \geq 0\)

\(\Leftrightarrow ab \geq a+b-1 = 2-c\)

\(\Leftrightarrow 3abc \geq 6c-3c^2\)

\(\Leftrightarrow c^2+ 3abc \geq 2c(3-c) = 2c(a+b) = 2ac + 2bc\)

Lại có: \(a^2 + b^2 \geq 2ab\)

Cộng vế theo vế 2 BĐT trên, ta có:

\(a^2+b^2+c^2+3abc \geq 2(ab+bc+ca)\)

hay BĐT (*) đúng. Tức là ta có đpcm.

Dấu bằng xảy ra ⇔ a = b = c = 1.

(Nếu không thấy lời giải, các em bấm F5 để cập nhật lại hoặc có thể vào đây đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 Chuyên KHTN )

-/-

Các môn thi khác

• Đề thi tuyển sinh vào lớp 10 môn Văn năm 2020 Chuyên KHTN

• Đề thi tuyển sinh vào lớp 10 môn Toán (vòng 2) năm 2020 Chuyên KHTN

• Đề thi vào lớp 10 môn Sinh Chuyên KHTN năm 2020

• Đề thi vào lớp 10 môn Hóa học Chuyên KHTN năm 2020

• Đề thi vào lớp 10 môn Vật lý Chuyên KHTN năm 2020

      Trên đây là toàn bộ nội dung của đáp án đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 của Chuyên KHTN được Đọc Tài Liệu thực hiện sau khi kì thi chính thức diễn ra. Với nội dung này các em có thể so sánh đối chiếu kết quả bài thi của mình!

   Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành hữu ích với bạn trong kỳ thi này.