Đáp án đề thi vào lớp 10 môn Toán không chuyên năm 2020 PTNK

NEW : Đề thi toán không chuyên vào lớp 10 PTNK 2021

Đề thi tuyển sinh vào lớp 10 môn Toán không chuyên năm 2020 của trường Phổ thông năng khiếu và đáp án được ĐọcTàiLiệu cập nhật giúp các em học sinh tham khảo, so sánh kết quả với bài thi của mình.

Đề thi vào lớp 10 năm 2020

Chi tiết đề thi vào lớp môn Toán không chuyên tuyển sinh lớp 10 PTNK như sau:

Đáp án đề tuyển sinh vào lớp 10 môn Toán không chuyên 2020

Cùng tham khảo đáp án chi tiết toán vào lớp 10 PTNK năm nay nhé:

Bài 1:

a)

(ĐKXĐ: \(x \geq 0\))

Khi M = x - 4, ta có:

\(M = \dfrac{x\sqrt x - 8}{3 + (\sqrt x + 1)^2} = x-4\)

\(\Leftrightarrow x\sqrt x - 8=( x-4)[3 + (\sqrt x + 1)^2]\)

\(\Leftrightarrow (\sqrt x-2)(x+2\sqrt x+4)=( \sqrt x-2)( \sqrt x+2)(x+2\sqrt x + 4)\)

\(\Leftrightarrow ( \sqrt x-2)(x+2\sqrt x + 4)( \sqrt x+2-1) = 0\)

\(\Leftrightarrow ( \sqrt x-2)(x+2\sqrt x + 4)( \sqrt x+1) = 0\)

Dễ thấy \(\sqrt x+1 > 0\) và

\(x+2\sqrt x + 4 = (\sqrt x+1)^2 + 3 > 0\)

\(\Rightarrow \sqrt x-2= 0\)

\(\Leftrightarrow x = 4\) (tm đkxđ)

KL...

b)

(ĐKXĐ: \(x \geq 0; x≠ 4\))

Ta có:

\(Q = M.N + P \)

\(=\dfrac{x\sqrt x - 8}{3 + (\sqrt x + 1)^2} . \dfrac{(\sqrt x + 1)^3 -(\sqrt x - 1)^3 }{(x-4)(3x+1)} + \dfrac{\sqrt x}{2+ \sqrt x}\)

\(=\dfrac{( \sqrt x-2)(x+2\sqrt x + 4)}{x+2\sqrt x + 4} . \dfrac{2[(\sqrt x+1)^2+(\sqrt x+1)(\sqrt x-1)+(\sqrt x-1)^2] }{(x-4)(3x+1)} + \dfrac{\sqrt x}{2+ \sqrt x}\)

\(=(\sqrt x-2). \dfrac{2(2x+2+x-1) }{(\sqrt x-2)(\sqrt x+2)(3x+1)} + \dfrac{\sqrt x}{2+ \sqrt x}\)

\(=\dfrac{2 }{\sqrt x+2} + \dfrac{\sqrt x}{2+ \sqrt x} = 1\)

KL: Q = 1.

Bài 2:

a)

\((x^4 + 4x^2 - 5) \left( \dfrac{x-3+\sqrt{3+x}}{\sqrt x -1} \right) = 0\)

ĐKXĐ: \(x \geq 0; x≠ 1\)

\(\Leftrightarrow (x^2+5)(x^2-1)(x-3+\sqrt{3+x}) = 0\)

\(\Leftrightarrow (x^2+5)(x^2-1)(x+3+\sqrt{3+x} - 6) = 0\)

\(\Leftrightarrow (x^2+5)(x^2-1)(\sqrt{3+x} - 2)(\sqrt{3+x} +3) = 0\)

Với \(x \geq 0; x≠ 1\) thì

\(\left\{ \matrix{ x^2 + 5 > 0 \hfill \cr \sqrt{3+x} +3 > 0 \hfill \cr} \right.\)

\(\Rightarrow \left[ \matrix{ x^2-1 = 0 \hfill \cr \sqrt{3+x} - 2 = 0 \hfill \cr} \right.\)

\(\Leftrightarrow \left[ \matrix{ x = 1 & (loại) \hfill \cr x = -1 & (loại) \hfill \cr x = 1 & (loại) \hfill \cr} \right.\)

KL: PT vô nghiệm.

b)

Vì (d) và (d1) cắt nhau tại I(3;9) nên tọa độ điểm I thỏa mãn phương trình của cả (d) và (d1), tức là:

\(\left\{ \matrix{ 9 = 3m + m \hfill \cr 9 = 3 + 3m + 2n - mn \hfill \cr} \right.\)

\(\Leftrightarrow \left\{ \matrix{ m = \dfrac{9}4 \hfill \cr 9 = 3 + 3.\dfrac{9}4 + 2n - \dfrac{9n}4 \hfill \cr} \right.\)

\(\Leftrightarrow \left\{ \matrix{ m = \dfrac{9}4 \hfill \cr n = 3 \hfill \cr} \right.\)

\(⇒ m.n = \dfrac{27}4\)

và \( \dfrac{m}n= \dfrac{3}4\).

KL....

c)

Gọi a, b lần lượt là chiều dài và rộng của hình chữ nhật (a > b > 0)

Ta có:

\(\left\{ \matrix{ 2a + 2b =28 \hfill \cr a^2+b^2 = (2R)^2 = 100 \hfill \cr} \right.\)

\(\Leftrightarrow \left\{ \matrix{ a = 14- b \hfill \cr (14-b)^2+b^2 = 100 \hfill \cr} \right.\)

\(\Leftrightarrow \left\{ \matrix{ a = 14- b \hfill \cr \left[ \matrix{ b=8 ⇒ a = 6 & (loại) \hfill \cr b = 6 ⇒ a = 8 & (tm) \hfill \cr} \right. \hfill \cr} \right.\)

Diện tích ABCD là:

\(S_{ABCD} = a.b = 48 \space ({cm}^2)\)

KL....

Bài 3:

a)

Xét phương trình hoành độ giao điểm của (P) và (d), ta có:

\(x^2 = 2mx + 3\)

\(\Leftrightarrow x^2 - 2mx - 3= 0\)  (*)

Ta có: \(\Delta' = m^2 + 3 \geq 3 > 0\)

suy ra (*) luôn có hai nghiệm phân biệt, hay (d) luôn cắt (P) tại 2 điểm phân biệt (đpcm).

Áp dụng hệ thức Vi-ét cho (*) ta có:

\(\left\{ \matrix{ x_1+x_2 = 2m \hfill \cr x_1x_2 = -3 \hfill \cr} \right.\)

Ta có:

\(y_1+y_2 = 2mx_1 + 3 + 2mx_2 + 3 = 2m (x_1+x_2) + 6\)

\(= 4m^2+ 6\)

b)

Ta có:

\(y_1 - 4y_2 = x_1 - 4x_2 + 3x_1x_2\)

\(\Leftrightarrow 2mx_1+3 - 4(2mx_2+3 )= x_1 - 4x_2 + 3.(-3)\)

\(\Leftrightarrow 2mx_1+3 - 8mx_2-12= x_1 - 4x_2 -9\)

\(\Leftrightarrow (2m-1)x_1- 4(2m-1)x_2= 0\)

\(\Leftrightarrow (2m-1)(x_1- 4x_2)= 0\)

\(\Leftrightarrow \left[ \matrix{ 2m-1 = 0 \hfill \cr x_1- 4x_2 = 0 \hfill \cr} \right.\)

\(\Leftrightarrow \left[ \matrix{ m = \dfrac{1}2 \hfill \cr x_1=4x_2 \hfill \cr} \right.\)

Với \(x_1 = 4x_2 \), thay vào ta có:

\(x_1x_2 = -3 = 4x_2^2 \) ⇒ vô nghiệm.

KL...

Bài 4:

a)

Gọi lượng gạo kho nhập ngày thứ nhất là A (tấn, A > 0)

Lượng gạo kho hàng nhập ngày thứ hai là: A x 120% = 1,2 A (tấn)

Lượng gạo kho hàng nhập ngày thứ ba là: 1,2 A x 120% = 1,44 A (tấn)

Sau ngày thứ ba, lượng gạo kho hàng có là: A+ 1,2 A + 1,44 A = 3,64 A (tấn)

Vì ngày thứ 3, sau khi nhập xong thì kho có 91 tấn nên:

3,64 A = 91 ⇒ A = 25 (tấn) (tm đk)

KL...

b)

Lượng gạo kho hàng nhập ngày thứ tư là: 1,44 A x 120% = 1,728 A (tấn)

Sau ngày thứ tư, lượng gạo kho hàng có là: 3,64 A + 1,728 A = 5,368 A (tấn)

Số gạo xuất ngày thứ 5 là: \(\dfrac{1}{10}.5,368 A = 0,6368 A\) (tấn)

Số gạo ngày thứ 6 xuất là:

\(\dfrac{1}{10}.(5,368 A - 0,6368 A) = 0,48312 A\) (tấn)

Vì tổng số gạo đã xuất của ngày 5 và 6 là 50,996 nên:

0,6368 A + 0,48312 A = 50,996

⇔ A = 50 (tấn) (tmđk)

KL....

Bài 5:

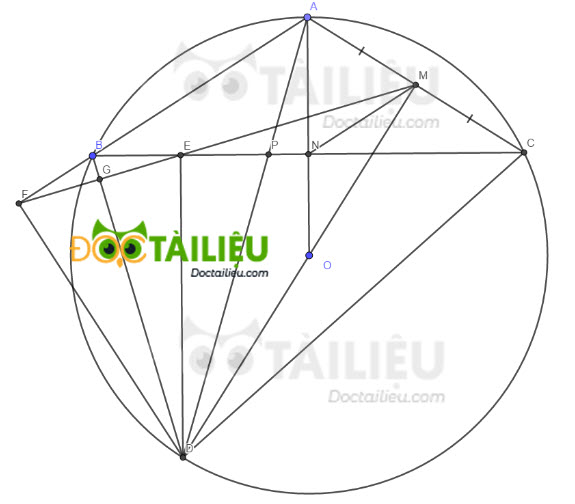
a)

Vì M là trung điểm của AC nên OM ⊥ AC.

Vì AB = AC ⇒ △ABC cân tại A ⇒ AO ⊥ BC

Suy ra ∠ONC = ∠OMC = 90° ⇒ tứ giác OCMN nội tiếp (đpcm).

Dễ thấy OM là trung trực của AC, D ∈ OM ⇒ DA = DC hay △DAC cân tại D, có DM là trung trực

\(⇒ ∠ADM = ∠MDC = \dfrac{1}2 ∠ADC\)  (1)

Vì AB = AC ⇒ \(\stackrel\frown{AB} = \stackrel\frown{AC}\) \(⇒ ∠BDA= ∠ADC= \dfrac{1}2 ∠BDC\)  (2)

Từ (1) và (2) suy ra \(∠ODC= ∠MDC = \dfrac{1}4 ∠BDC\)

hay ∠BDC = 4.∠ODC (đpcm).

b)

Vì △DAC cân tại D (cmt) ⇒ ∠DAC = ∠DCA \(= ∠MDC = \dfrac{1}2(\stackrel\frown{AB} + \stackrel\frown{BD})\)

Lại có  \(∠APC= \dfrac{1}2(\stackrel\frown{AC} + \stackrel\frown{BD}) =\dfrac{1}2(\stackrel\frown{AB} + \stackrel\frown{BD}) = ∠DAC\)

Hay ∠APC = ∠PAC ⇒ △PCA cân tại C ⇒ CA = CP (đpcm).

Gọi BD cắt ME tại G.

Ta thấy ∠DBP = ∠DAC (góc nội tiếp cùng chắn cung DC) = ∠APC (cmt) = ∠BPD (góc đối đỉnh) ⇒ △DBP cân tại D.

△DBP cân tại D có DE là phân giác ⇒ DE ⊥ BP và

\(∠BDE= ∠EDP= \dfrac{1}2 ∠BDP\).

Ta thấy ∠DEC = ∠DMC = 90° ⇒ tứ giác DEMC nội tiếp ⇒ ∠EMD = ∠ECD (góc nội tiếp cùng chắn cung ED)

hay ∠GMD = ∠ECD.

Lại có ∠EDC = 3.∠ODC = ∠BDM = ∠GDM.

Xét △GDM và △EDC có:

∠GMD = ∠ECD (cmt)

∠EDC = ∠GDM

Suy ra △GDM ∽ △EDC ⇒ ∠MGD = ∠CED = 90° ⇒ ME vuông góc với DB (đpcm).

c)

Vì ABDC nội tiếp (O) ⇒ ∠ABD + ∠ACD = 180°

⇒ ∠ACD = 180° - ∠ABD = ∠FBG  (3)

Lại có ∠GBE = ∠DBC = ∠DAC (góc nội tiếp cùng chắn cung DC) = ∠ACD (cmt)  (4)

Từ (3) và (4) suy ra ∠FBG = ∠GBE ⇒ BG là phân giác của góc FBE.

Xét △FBE có BG vừa là đường cao vừa là phân giác ⇒ △FBG cân tại B ⇒ FB = EB và ∠BFE = ∠BEF = ∠MEN (đối đỉnh).

Dễ thấy N là trung điểm của BC ⇒ MN là đường trung bình của △CBA ⇒ MN // AB ⇒ ∠EMN = ∠EFB (góc sole trong) = ∠MEN (cmt)

⇒ △MNE cân tại N (đpcm).

Xét △BFD và △BED có:

∠FBD = ∠EBD (cmt)

Cạnh BD chung

BF = BE (cmt)

Suy ra △BFD = △BED ⇒ DE = DF ⇒ \(\dfrac{DE}{DF} = 1\).

-/-

Các môn thi khác

• Đề thi tuyển sinh vào lớp 10 2020 môn Văn không chuyên PTNK

• Đề thi tuyển sinh vào lớp 10 2020 môn Anh không chuyên PTNK

Trên đây là toàn bộ nội dung của đáp án đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 của PTNK (HCM) được Đọc Tài Liệu thực hiện sau khi kì thi chính thức diễn ra. Với nội dung này các em có thể so sánh đối chiếu kết quả bài thi của mình!

Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành hữu ích với bạn trong kỳ thi này.