NEW: Đề thi tuyển sinh lớp 10 môn Toán Kon Tum
Đáp án đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 Kon Tum được ĐọcTàiLiệu cập nhật giúp các em học sinh tham khảo, so sánh kết quả với bài thi của mình.
Đề thi vào lớp 10 năm 2020
Chi tiết đề thi vào lớp 10 môn Toán của tỉnh Kon Tum như sau:
Sở GD&ĐT Kon Tum ĐỀ CHÍNH THỨC | KỲ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC: 2020 - 2021 Môn: Toán |

Đáp án đề tuyển sinh vào lớp 10 môn Toán Kon Tum 2020
Dự kiến: Đáp án đề thi tuyển sinh lớp 10 môn Toán năm 2020 Kon Tum sẽ được cập nhật sau khi kết thúc thời gian thi chính thức 30 - 40 phút

Câu 5
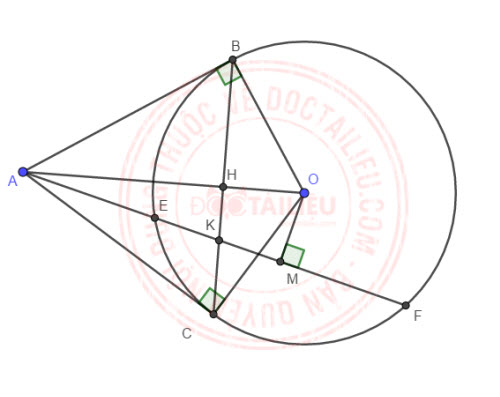
a)
Vì AB, AC là tiếp tuyến tại B, C của (O) ⇒ ∠ABO = ∠ACO = 90° ⇒ Tứ giác ABOC nội tiếp đường tròn đường kính AO (đpcm).
b)
Dễ thấy AO ⊥ BC tại H.
Áp dụng hệ thức lượng trong △ABO vuông tại B, có đường cao BH:
AH.AO = AB² (1)
Xét △ABE và △AFB, ta có:
Góc ∠EAB chung
∠ABE = ∠BEF = ∠AFB (t/c góc tạo bởi tiếp tuyến và dây cung)
Suy ra △ABE ∽ △AFB ⇒ \(\dfrac{AB}{AE} = \dfrac{AF}{AB}\) ⇒ AE.AF = AB² (2)
Từ (1) và (2) suy ra AH.AO = AE.AF (đpcm).
c)
Vì M là trung điểm EF ⇒ OM ⊥ EF ⇒ ∠OMK = 90° = ∠OHK.
Xét △AHK và △AMO, ta có:
Góc ∠HAK chung
∠KHA = ∠OMA = 90° (cmt)
Suy ra △AHK ∽ △AMO ⇒ \(\dfrac{AH}{AK} = \dfrac{AM}{AO}\) ⇒ \(AK = \dfrac{AH.AO}{AM} \)
Ta có:
\(\dfrac{AK}{AE} + \dfrac{AK}{AF} = \dfrac{AK(AE+AF)}{AE.AF} = \dfrac{\dfrac{AH.AO}{AM}.(AE+AF)}{AH.AO}\)
\(= \dfrac{AE+AF}{AM} = \dfrac{AM - EM +AM + MF}{AM} = \dfrac{2AM}{AM} =2\)
Hay \(\dfrac{AK}{AE} + \dfrac{AK}{AF} = 2\) (đpcm).
Câu 6
\(\dfrac{1-\sqrt{x-2019}}{x-2019} + \dfrac{1-\sqrt{y-2020}}{y-2020} + \dfrac{1-\sqrt{z-2021}}{z-2021} + \dfrac{3}4 = 0\)
ĐKXĐ: x > 2019; y > 2020; z > 2021.
\(⇔ \dfrac{1-\sqrt{x-2019}}{x-2019} +\dfrac{1}4 + \dfrac{1-\sqrt{y-2020}}{y-2020} + \dfrac{1}4 + \dfrac{1-\sqrt{z-2021}}{z-2021} + \dfrac{1}4 = 0\)
\(⇔ \dfrac{(2-\sqrt{x-2019})^2}{4(x-2019)} + \dfrac{(2-\sqrt{y-2020})^2}{4(y-2020)} + \dfrac{(2-\sqrt{z-2021})^2}{4(z-2021)}= 0\)
Dễ thấy VT của PT trên luôn ≥ 0 với mọi x > 2019; y > 2020; z > 2021.
Vậy phương trình có nghiệm
\(⇔ 1- \sqrt{x-2019} =1- \sqrt{y-2020} = 1- \sqrt{z-2021} =0\)
\(⇔ \sqrt{x-2019} =\sqrt{y-2020} = \sqrt{z-2021} =1\)
\(⇔ \left\{ \matrix{ x = 2020 \hfill \cr y = 2021 \hfill \cr z = 2022 \hfill \cr} \right.\) (tm đkxđ).
KL...
-/-
Các môn thi khác
• Đề thi tuyển sinh vào lớp 10 môn Văn năm 2020 Kon Tum
• Đề thi tuyển sinh vào lớp 10 môn Anh năm 2020 Kon Tum
Trên đây là toàn bộ nội dung của đáp án đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 của tỉnh Kon Tum được Đọc Tài Liệu thực hiện sau khi kì thi chính thức diễn ra. Với nội dung này các em có thể so sánh đối chiếu kết quả bài thi của mình!
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành hữu ích với bạn trong kỳ thi này.
