Bài 5 trang 45 SGK Toán 9 tập 1

Để giải bài 5 trang 45 SGK Toán 9 tập 1 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết, không chỉ tham khảo cách làm hoặc đáp án mà bài viết này còn giúp bạn nắm vững lại các kiến thức Toán 9 bài 1 để tự tin giải tốt các bài tập về hàm số.

Đề bài 5 trang 45 SGK Toán 9 tập 1

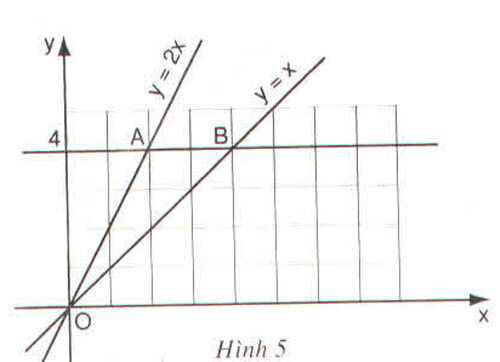
a) Vẽ đồ thị hàm số y = x và y = 2x trên cùng một mặt phẳng tọa độ Oxy.

b) Đường thẳng song song với trục Ox và cắt trục Oy tại điểm có tung độ y = 4 lần lượt cắt các đường thẳng y = 2x, y = x tại 2 điểm A và B.

Tìm tọa độ của các điểm A, B và tính chu vi, diện tích của tam giác OAB theo đơn vị đo trên các trục tọa độ là cm.

» Bài tập trước: Bài 4 trang 45 SGK Toán 9 tập 1

Giải bài 5 trang 45 SGK Toán 9 tập 1

Hướng dẫn cách làm

a) Cách vẽ đồ thị hàm số \(y=ax,\ (a \ne 0)\):  Cho \(x=x_0 \Rightarrow y_0=ax_0\)

Đồ thị hàm số \(y=ax\, \, (a\neq 0)\) là đường thẳng đi qua gốc tọa độ và điểm \(A(x_0;y_0)\)

b) +) Đường thẳng song song với trục Ox cắt trục Oy tại điểm có tung độ y=b có phương trình đường thẳng là y=b

+) Muốn tìm tọa độ giao điểm của hai đường thẳng \(y=ax\) và \(y=a'x\) ta giải phương trình \(ax=a'x\) tìm được hoành độ. Thay hoành độ vào một trong hai đường thẳng trên tìm được tung độ.

+) Sử dụng đinh lí Py - ta - go trong tam giác vuông: \(\Delta ABC\)  vuông tại \(A\) thì \(AB^2+ AC^2 =BC^2\)

+) Chu vi tam giác: \(C_{∆OAB}= AB+BO+AO\)

+) Diện tích \(\Delta ABC\) có đường cao \(h\)  và \(a\) là độ dài cạnh ứng với đường cao: \(S_{∆OAB}=\dfrac{1}{2}.h.a\)

Đáp án chi tiết

Dưới đây là các cách giải bài 5 trang 45 SGK Toán 9 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

a) Xem hình trên và vẽ lại

b)

+) Ta có mỗi ô vuông trên hình 5 là một hình vuông có cạnh là 1cm.

Từ hình vẽ ta xác định được: \(A(2; 4),\ B(4; 4)\)

+) Tính độ dài các cạnh của \(∆OAB\)

Dễ thấy \(AB = 4 - 2 = 2 (cm)\)

Áp dụng định lý Py-ta-go, ta có:

\(\eqalign{ & OA = \sqrt {{2^2} + {4^2}} = 2\sqrt 5 \left( {cm} \right) \cr & OB = \sqrt {{4^2} + {4^2}} = 4\sqrt 2 \left( {cm} \right) \cr} \)

\(\Rightarrow\) Chu vi \(\Delta OAB\) là:

\(C_{\Delta OAB}=OA + OB + AB \)

\(=2+ 2\sqrt 5 + 4\sqrt 2  \approx  12,13(cm)\)

+) Tính diện tích \(∆OAB\)

Gọi \(C\) là điểm biểu diễn số \(4\) trên trục tung, ta có:

Cách 1:

\(\eqalign{ & {S_{\Delta OAB}} = {S_{\Delta OBC}} - {S_{\Delta OAC}} \cr & = {1 \over 2}OC.BC - {1 \over 2}OC.AC \cr & = {1 \over 2}{.4^2} - {1 \over 2}.4.2 = 8 - 4 = 4\left( {c{m^2}} \right) \cr} \)

Cách 2: 

\(∆OAB\) có đường cao ứng với cạnh AB là OC.

\(\Rightarrow S_{∆OAB}=\dfrac{1}{2}.OC.AB=\dfrac{1}{2}.4.2=4 (cm^2)\)

» Bài tập tiếp theo: Bài 6 trang 45 SGK Toán 9 tập 1

Nội dung trên đã giúp bạn nắm được cách làm bài 5 trang 45 SGK Toán 9 tập 1. Hy vọng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ giúp các bạn hoàn thành bài tập chính xác và học tốt môn học này.