Bài 2 trang 40 sgk hình học lớp 10

Đề bài

Cho \(A O B\) là tam giác cân tại \(O\) có \(O A=a\) và có các đường cao \(O H\) và \(A K\). Giả sử \(\widehat{A O H}=\alpha .\) Tính \(A K\) và \(O K\) theo \(a\) và \(\alpha\)

Giải bài 2 trang 40 sgk hình học lớp 10

Hướng dẫn cách giải

+) Sử dụng công thức lượng giác đối với góc nhọn ta có:

\(\sin \alpha=\frac{cạnh \text { đối }}{c a n h \text { huyền }}\) và \(\cos \alpha=\frac{\operatorname{cạnh\ kề}}{\operatorname{cạnh \ huyền }}\)

Bài làm

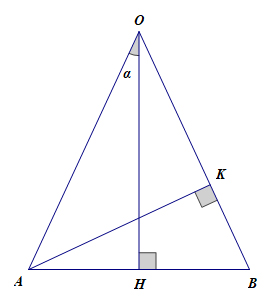
TH1: \(\alpha < 45^0\)

Do tam giác \(OAB\) cân tại \(O\) nên ta có \(\widehat {AOB} = 2\widehat {AOH}=2\alpha < 90^0 \)

Tam giác \(OKA\) vuông tại \(K\) nên ta có:

\(\sin \widehat {AOK} = \frac{{AK}}{{OA}}  \)

\(\Rightarrow AK = OA.\sin \widehat {AOK} \)\(\Rightarrow AK = a.\sin 2\alpha. \)

\(\cos \widehat {AOK} = \frac{{OK}}{{OA}}  \)

\(\Rightarrow OK = OA.cos\widehat {AOK} \)\(\Rightarrow OK = a.\cos 2\alpha .\)

TH2: \(\alpha > 45^0\)

Do tam giác \(OAB\) cân tại \(O\) nên ta có \(\widehat {AOB} = 2\widehat {AOH}=2\alpha > 90^0 \)

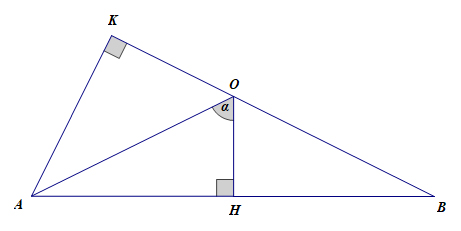
Tam giác AKO vuông tại K có AO=a, \(\widehat {AOK} = {180^0} - \widehat {AOB} = {180^0} - 2\alpha \)

Khi đó:

\(\begin{array}{l}\sin \widehat {AOK} = \frac{{AK}}{{OA}}\\ \Rightarrow AK = OA\sin \widehat {AOK}\\ = a\sin \left( {{{180}^0} - 2\alpha } \right) = a\sin 2\alpha \\\cos \widehat {AOK} = \frac{{OK}}{{OA}}\\ \Rightarrow OK = OA\cos \widehat {AOK}\\ = a\cos \left( {{{180}^0} - 2\alpha } \right) =  - a\cos 2\alpha \end{array}\)