Bài 3.32 trang 59 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Chứng minh rằng: Cho điểm A và đường thẳng d thì có duy nhất đường thẳng đi qua A và vuông góc với d, tức là nếu có hai đường thẳng đi qua A vuông góc với d thì chúng phải trùng nhau.
Bài giải
Giả sử có 2 đường thẳng a và a’ đi qua A và vuông góc với d.
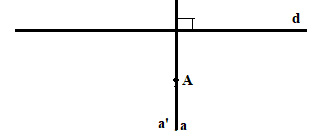
Vì a \( \bot \)d, mà a’ \( \bot \)d nên a // a’ (hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Mà A \( \in \)d, A \( \in \)d’
\( \Rightarrow a \equiv a'\)
Vậy có duy nhất đường thẳng đi qua A và vuông góc với d
Bài 3.33 trang 59 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Vẽ ba đường thẳng phân biệt a,b,c sao cho a//b, b//c và hai đường thẳng phân biệt m, n cùng vuông góc với a. Hỏi trên hình có bao nhiêu cặp đường thẳng song song, có bao nhiêu cặp đường thẳng vuông góc?
Bài giải
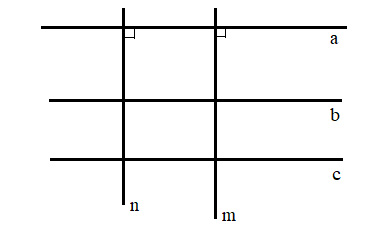
Ta có: +) a // b, b // c nên a // c ( Hai đường thẳng cùng song song với đường thẳng thứ ba thì chúng song song với nhau)
+) m \( \bot \) a; n \( \bot \)a nên m // n (Hai đường thẳng cùng vuông góc với một đường thẳng thứ ba thì song song với nhau)
Theo định lý “Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng vuông góc với đường thẳng kia, ta có:
+) a // b; a \( \bot \)n nên b \( \bot \)n
+) a // b; a \( \bot \)m nên b \( \bot \)m
+) a // c; a \( \bot \)n nên c \( \bot \)n
+) a // c; a \( \bot \)m nên c \( \bot \)m
Vậy các cặp đường thẳng song song là: a // b ; a // c ; b // c; m // n
Các cặp đường thẳng vuôn góc là: b \( \bot \)n; b \( \bot \)m; c \( \bot \)n; c \( \bot \)m; a \( \bot \)n; a \( \bot \)m
Bài 3.34 trang 59 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Cho Hình 3.50, trong đó hai tia Ax và By nằm trên hai đường thẳng song song. Chứng minh rằng \(\widehat C = \widehat A + \widehat B\)
Bài giải
Qua C kẻ đường thẳng d song song với Ax
Vì Ax // By nên d // By
Vì d // Ax nên \(\widehat A = \widehat {{C_1}}\)(2 góc so le trong)
Vì d // By nên \(\widehat B = \widehat {{C_2}}\) (2 góc so le trong)
Mà \(\widehat C = \widehat {{C_1}} + \widehat {{C_2}}\)
Vậy \(\widehat C = \widehat A + \widehat B\)(đpcm)
Bài 3.35 trang 59 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Cho Hình 3.51, trong đó Ox và Ox’ là hai tia đối nhau
a) Tính tổng số đo ba góc O1, O2, O3 .
Gợi ý: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\), trong đó \(\widehat {{O_1}} + \widehat {{O_2}} = \widehat {x'Oy}\)
b) Cho \(\widehat {{O_1}} = 60^\circ ,\widehat {{O_2}} = 70^\circ \). Tính \(\widehat {{O_2}}\)
Bài giải
a) Ta có: \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = (\widehat {{O_1}} + \widehat {{O_2}}) + \widehat {{O_3}}\)=\(\widehat {x'Oy} + \widehat {{O_3}}\), mà \(\widehat {x'Oy} + \widehat {{O_3}}\)= 180\(^\circ \) ( 2 góc kề bù)
Vậy \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
b) Vì \(\widehat {{O_1}} + \widehat {{O_2}} + \widehat {{O_3}} = 180^\circ \)
\(\begin{array}{l} \Rightarrow 60^\circ + \widehat {{O_2}} + 70^\circ = 180^\circ \\ \Rightarrow \widehat {{O_2}} = 180^\circ - 60^\circ - 70^\circ = 50^\circ \end{array}\)
Vậy \(\widehat {{O_2}} = 50^\circ \)
Bài 3.36 trang 59 sgk toán 7 tập 1 Kết nối tri thức
Câu hỏi
Cho Hình 3.52, biết \(\widehat {xOy} = 120^\circ ,\widehat {yOz} = 110^\circ \). Tính số đo góc zOx.
Gợi ý: Kẻ thêm tia đối của tia Oy
Bài giải
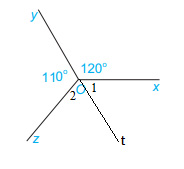
Kẻ Ot là tia đối của tia Oy.
Ta được:+) \(\widehat {{O_1}} + \widehat {xOy} = 180^\circ \) ( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow \widehat {{O_1}} + 120^\circ = 180^\circ \\ \Rightarrow \widehat {{O_1}} = 180^\circ - 120^\circ = 60^\circ \end{array}\)
+) \(\widehat {{O_2}} + \widehat {yOz} = 180^\circ \)( 2 góc kề bù)
Vì Ot nằm giữa 2 tia Ox và Oz nên \(\widehat {xOz} = \widehat {{O_1}} + \widehat {{O_2}} = 60^\circ + 70^\circ = 130^\circ \)
Vậy \(\widehat {zOx} = 130^\circ \)
Xem thêm:
- Trang 45 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 49 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 50 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 53 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 54 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 57 SGK Toán 7 tập 1 Kết nối tri thức
- Trang 58 SGK Toán 7 tập 1 Kết nối tri thức
Trên đây là chi tiết hướng dẫn Giải bài tập Trang 59 SGK Toán 7 tập 1 Kết nối tri thức được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Kết nối tri thức bởi Đọc Tài Liệu