Bạn đang tìm kiếm tài liệu tổng hợp kiến thức về Hình trụ - Hình nón - Hình cầu? Hãy tham khảo ngay bài viết dưới đây của Đọc tài liệu với những lý thuyết ôn tập chương 4 phần Hình học: Hình trụ - Hình nón - Hình cầu cùng tổng hợp các dạng toán cơ bản thường gặp. Đây sẽ là tài liệu học tập hữu ích cho học sinh và đồng thời giúp các thầy cô có thêm tài liệu hay phục vụ việc dạy học.
Cùng tham khảo nhé!

Kiến thức cần nắm về Hình trụ - Hình nón - Hình cầu
1. Hình trụ
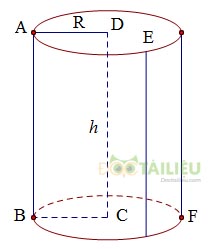
Cho hình trụ có bán kính đáy R và chiều cao h. Khi đó :
+ Diện tích xung quanh : \({S_{xq}} = 2\pi Rh\) .
+ Diện tích đáy : \({S_đ} = \pi {R^2}\).
+ Diện tích toàn phần : \({S_{tp}} = {S_{xq}} + 2.{S_đ} = 2\pi Rh + 2\pi {R^2}\) .
+ Thể tích : \( V = \pi {R^2}h\).
2. Hình nón
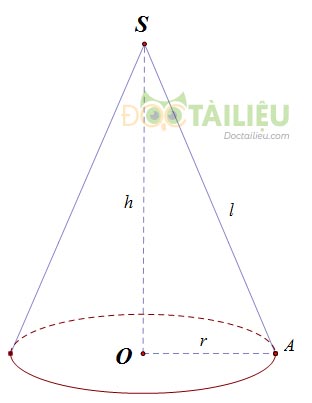
Cho hình nón có bán kính đáy R = OA, đường sinh l = SA, chiều cao h = SO. Khi đó :
+ Diện tích xung quanh: \({S_{xq}} = \pi Rl\).
+ Diện tích đáy : \({S_d} = \pi {R^2}\)
+ Diện tích toàn phần: \({S_{tp}} = {S_{xq}} + {S_đ} = \pi Rl + \pi {R^2}.\)
+ Thể tích: \(V = \dfrac{1}{3}\pi {R^2}h.\)
+ Công thức liên hệ : \({R^2} + {h^2} = {l^2}\)
3. Hình nón cụt
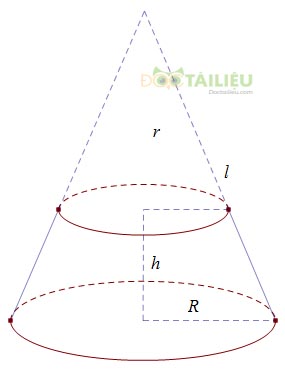
Cho hình nón cụt có các bán kính đáy là R và r, chiều cao h, đường sinh l.
+ Diện tích xung quanh: \({S_{xq}} = \pi (R + r)l\).
+ Diện tích toàn phần: \({S_{tp}} = \pi (R + r)l + \pi {R^2} + \pi {r^2}\).
+ Thể tích: \( V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2})\).
4. Hình cầu
Định nghĩa
- Khi quanh nửa hình tròn tâm O, bán kính R một vòng quanh đường kính AB cố định ta thu được một hình cầu.
- Nửa đường tròn trong phép quay nói trên tạo thành một mặt cầu.
- Điểm O gọi là tâm, R là bán kính của hình cầu hay mặt cầu đó.
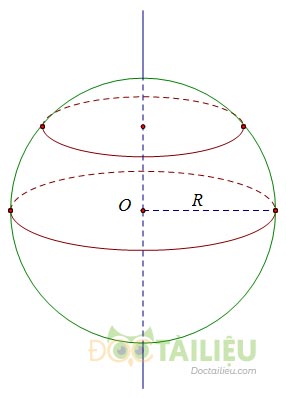
Chú ý:
- Khi cắt hình cầu bởi một mặt phẳng ta được một hình tròn.
- Khi cắt mặt cầu bán kính R bởi một mặt phẳng ta được một đường tròn, trong đó :
+ Đường tròn đó có bán kính R nếu mặt phẳng đi qua tâm (gọi là đường kính lớn).
+ Đường tròn đó có bán kính bé hơn R nếu mặt phẳng không đi qua tâm.
Diện tích và thể tích
Cho hình cầu bán kính R.
- Diện tích mặt cầu : \(S = 4\pi {R^2} .\)
- Thể tích hình cầu : \(V = \dfrac{4}{3}\pi {R^3}.\)
*****************
Hy vọng với hệ thống kiến thức lý thuyết ôn tập chương 4 phần Hình học: Hình trụ - Hình nón - Hình cầu trên đây, các em sẽ có thêm một tài liệu học tập hữu ích để học tốt hơn môn Toán 9. Chúc các em luôn học tốt và đạt kết quả cao!