Bài 1 trang 35 Toán 7 Cánh Diều tập 1
Câu hỏi
a) Đọc các số sau: \(\sqrt {15} ;\sqrt {27,6} ;\sqrt {0,82}\)
b) Viết các số sau: căn bậc hai số học của \(39\); căn bậc hai số học của \(\frac{9}{{11}};\) căn bậc hai số học của \(\frac{{89}}{{27}}\)
Bài giải
a) \(\sqrt {15}\) đọc là: căn bậc hai số học của mười lăm
\(\sqrt {27,6}\) đọc là: căn bậc hai số học của hai mươi bảy phẩy sáu
\(\sqrt {0,82}\) đọc là: căn bậc hai số học của không phẩy tám mươi hai
b) Căn bậc hai số học của \(39\) viết là: \(\sqrt {39}\)
Căn bậc hai số học của \(\frac{9}{{11}}\) viết là: \(\sqrt {\frac{9}{{11}}}\)
Căn bậc hai số học của \(\frac{{89}}{{27}}\) viết là: \(\sqrt {\frac{{89}}{{27}}}\)
Bài 2 trang 35 Toán 7 Cánh Diều tập 1
Câu hỏi
Chứng tỏ rằng:
a) Số 0,8 là căn bậc hai số học của số 0,64
b) Số -11 không phải là căn bậc hai số học của số 121
c) Số 1,4 là căn bậc hai số học của số 1,96 nhưng –1,4 không phải là căn bậc hai số học của số 1,96.
Bài giải
a) Vì \(0,8 > 0\) và \(0,{8^2} = 0,64\) nên số \(0,8\) là căn bậc hai số học của số \(0,64\)
b) Vì tuy \({( - 11)^2} = 121\) nhưng \(-11 < 0\) nên số \(-11\) không phải là căn bậc hai số học của số \(121\)
c) Vì \(1,{4^2} = 1,96\) và \(1,4 > 0\) nên số 1,4 là căn bậc hai số học của số \(1,96\)
Nhưng vì \(-1,4 < 0\) nên –1,4 không phải là căn bậc hai số học của số \(1,96\).
Bài 3 trang 35 Toán 7 Cánh Diều tập 1
Câu hỏi
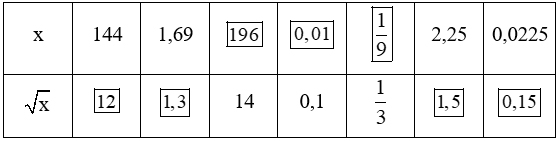
Tìm số thích hợp cho [?]

Bài giải
Bài 4 trang 35 Toán 7 Cánh Diều tập 1
Câu hỏi
Tính giá trị của biểu thức:
a) \(\sqrt {0,49} + \sqrt {0,64}\)
b) \(\sqrt {0,36} - \sqrt {0,81}\)
c) \(8.\sqrt 9 - \sqrt {64}\)
d) \(0,1.\sqrt {400} + 0,2.\sqrt {1600}\)
Bài giải
\(\begin{array}{l}a)\sqrt {0,49} + \sqrt {0,64} = 0,7 + 0,8 = 1,5;\\b)\sqrt {0,36} - \sqrt {0,81} = 0,6 - 0,9 = - 0,3;\\c)8.\sqrt 9 - \sqrt {64} = 8.3 - 8 = 24 - 8 = 16;\\d)0,1.\sqrt {400} + 0,2.\sqrt {1600} = 0,1.20 + 0,2.40 = 2 + 8 = 10\end{array}\)
Bài 5 trang 35 Toán 7 Cánh Diều tập 1
Câu hỏi
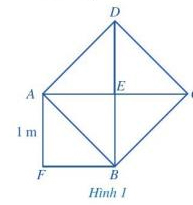
Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 m, hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.
a) Tính diện tích của hình vuông ABCD.
b) Tính độ dài đường chéo AB.
Bài giải
a) Ta có: \({S_{ABCD}} = 4.{S_{AEB}} = 4. \frac{1}{2}.1.1 = 2 (cm2)\)
b) AB = \(\sqrt {S{}_{ABCD}} = \sqrt 2 (cm)\)
Bài tiếp theo: Toán 7 Cánh Diều trang 42
Xem thêm:
- Toán 7 cánh diều trang 47
- Toán 7 cánh diều trang 51
- Toán 7 cánh diều trang 54
- Toán 7 cánh diều trang 58
- Toán 7 Cánh Diều trang 63
- Toán 7 Cánh Diều trang 68
- Toán 7 Cánh Diều trang 69
- Toán 7 Cánh Diều trang 70
Trên đây là chi tiết hướng dẫn Giải bài tập Toán 7 Cánh Diều trang 35 được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Hướng dẫn giải Toán 7 Cánh Diều bởi Đọc Tài Liệu