Bài 1 trang 104 Toán 7 Cánh Diều tập 1
Câu hỏi
Quan sát hình 44, biết a // b.
a) So sánh \(\widehat {{M_1}}\) và \(\widehat {{N_3}}; \widehat {{M_4}}\) và \(\widehat {{N_2}}\) ( mỗi cặp góc M1 và N3, M4 và N2 gọi là một cặp góc so le ngoài)
b) Tính: \(\widehat {{M_2}} + \widehat {{N_1}}\) và \(\widehat {{M_3}} + \widehat {{N_4}}\) ( mỗi cặp góc M2 và N1, M3 và N4 gọi là một cặp góc trong cùng phía)
Bài giải
a) Vì a // b nên\(\widehat {{M_1}} = \widehat {{N_1}} ; \widehat {{M_4}} = \widehat {{N_4}}\) ( 2 góc đồng vị) mà \(\widehat {{N_3}} = \widehat {{N_1}} ; \widehat {{N_4}} = \widehat {{N_2}}\) ( 2 góc đối đỉnh) nên \(\widehat {{M_1}} =\widehat {{N_3}}; \widehat {{M_4}} =\widehat {{N_2}}\)
b) Vì a // b nên \(\widehat {{M_2}} = \widehat {{N_2}};\widehat {{M_3}} = \widehat {{N_3}}\) ( 2 góc đồng vị), mà \(\widehat {{N_1}} + \widehat {{N_2}} = 180^\circ ;\widehat {{N_3}} + \widehat {{N_4}} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {{M_2}} + \widehat {{N_1}} = 180^\circ ; \widehat {{M_3}} + \widehat {{N_4}}= 180^\circ \)
Chú ý:
Nếu đường thẳng c cắt cả hai đường thẳng song song a và b thì:
- Hai góc so le ngoài bằng nhau
- Hai góc trong cùng phía có tổng số đo bằng \(180^\circ \)
Bài 2 trang 104 Toán 7 Cánh Diều tập 1
Câu hỏi
Quan sát Hình 45.
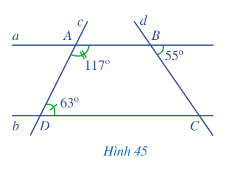
a) Vì sao hai đường thẳng a và b song song với nhau?
b) Tính số đo góc BCD.
Bài giải
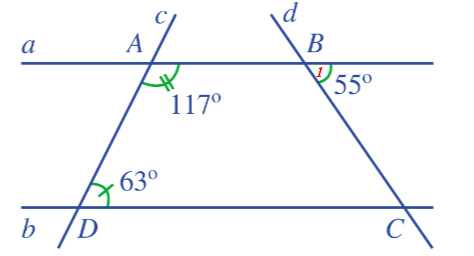
a) Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) ( 2 góc kề bù) nên \(117^\circ + \widehat {{A_2}} = 180^\circ \Rightarrow \widehat {{A_2}} = 180^\circ - 117^\circ = 63^\circ \)
Vì \(\widehat {{A_2}} = \widehat {{D_1}}\) ( cùng bằng 63 độ)
Mà 2 góc này ở vị trí đồng vị
\( \Rightarrow a // b\) ( đpcm)
b) Vì a // b nên \(\widehat {{B_1}} = \widehat {BCD}\)( 2 góc so le trong), mà \(\widehat {{B_1}} = 55^\circ \Rightarrow \widehat {BCD} = 55^\circ \)
Bài 3 trang 104 Toán 7 Cánh Diều tập 1
Câu hỏi
Để đảm bảo an toàn khi đi lại trên cầu thang của ngôi nhà, người ta phải làm lan can. Phía trên của lan can có tay vịn làm chỗ dựa để khi lên xuống cầu thang được thuận tiện. Phía dưới tay vịn là các thanh trụ song song với nhau và các thanh sườn song song với nhau. Để đảm bảo chắc chắn thì các thanh trụ của lan can được gắn vuông góc cố định xuống bậc cầu thang.
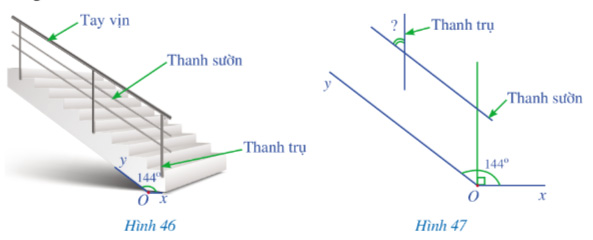
Trong Hình 46, góc xOy bằng \(144^\circ \). Hỏi góc nhọn tạo bởi một thanh sườn với một thanh trụ của lan can là bao nhiêu độ?
Bài giải
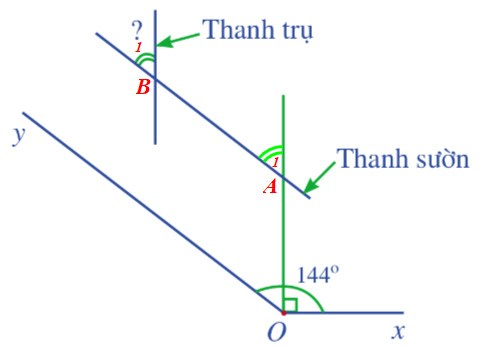
Vì AB // Oy nên \(\widehat {xOy} = \widehat {{A_1}}\)( 2 góc đồng vị), mà \(\widehat {xOy} = 144^\circ \Rightarrow \widehat {{A_1}} = 144^\circ \)
Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ \) ( 2 góc kề bù) nên \(\widehat {{A_2}} + 144^\circ = 180^\circ \Rightarrow \widehat {{A_2}} = 180^\circ - 144^\circ = 36^\circ \)
Vì a // b nên \(\widehat {{B_1}} = \widehat {{A_2}}\) ( 2 góc đồng vị), mà \(\widehat {{A_2}} = 36^\circ \Rightarrow \widehat {{B_1}} = 36^\circ \)
Trên đây là chi tiết hướng dẫn Giải bài tập Toán 7 Cánh Diều trang 104 được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 7
Xem tiếp: Toán 7 Cánh Diều trang 107
Xem thêm:
Hướng dẫn giải Toán 7 Cánh Diều bởi Đọc Tài Liệu