Hướng dẫn trả lời câu hỏi và giải bài tập Toán 8 Cánh Diều tập 2 giúp học sinh nắm được các cách giải bài tập Chương 8: Ứng dụng của định lí Thalès trong tam giác chuẩn bị bài trước khi tới lớp và luyện tập giải toán tại nhà.
Chương 8 Bài 2: Ứng dụng của định lí Thalès trong tam giác
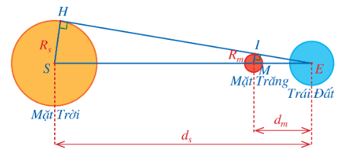
Khởi động trang 58 Toán 8 Tập 2: Từ xa xưa, con người đã muốn tìm hiểu về Mặt Trời, Trái Đất, Mặt Trăng, chẳng hạn: Đường kính của mỗi hành tinh đó là bao nhiêu? Khoảng cách từ Trái Đất đến Mặt Trăng và Mặt Trời là bao nhiêu? Dựa vào hiện tượng Nhật thực và Nguyệt thực, các nhà toán học và thiên văn học Hy Lạp cổ đại đã đưa ra được câu trả lời cho những vấn đề trên.
Vào thời điểm xảy ra Nhật thực (Nguyệt thực), đường kính của Mặt Trời và Mặt Trăng có tỉ lệ với khoảng cách từ Trái Đất đến Mặt Trời và đến Mặt Trăng hay không?
Lời giải:
Hình vẽ trên mô tả vị trí tương đối của Mặt Trời, Mặt Trăng và Trái Đất khi xảy ra hiện tượng Nhật thực.
Gọi khoảng cách từ Trái Đất đến Mặt Trời, Mặt Trăng lần lượt là \(d_S = ES\); \(d_m = EM\).
Gọi bán kính của Mặt Trời, Mặt Trăng lần lượt là \(R_S = SH\) và \(R_M = MI\)
Xét tam giác EHS, ta có \(\widehat{EIM} = \widehat{EHS} = 90°\) nên MI//SH
Do đó, áp dụng hệ quả của định lí Thalès, ta có: \(\dfrac{MI}{SH} = \dfrac{EM}{ES}\)
Vậy \(\dfrac{d_m}{d_S} = \dfrac{R_m}{R_S}\), hay vào thời điểm xảy ra Nhật thực, đường kính của Mặt Trời và Mặt Trăng tỉ lệ với khoảng cách từ Trái Đất đến Mặt Trời và đến Mặt Trăng.
Ta cũng có kết quả trên tương ứng với thời điểm xảy ra Nguyệt thực.
I. Ước lượng khoảng cách
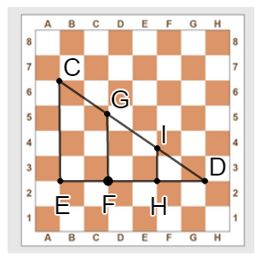
Luyện tập 1 trang 59 Toán 8 Tập 2: Bạn Loan đặt một cái que lên bàn cờ vua như ở Hình 20. Bạn ấy nói rằng: Không sử dụng thước đo, có thể chia cái que đó thành ba phần bằng nhau. Em hãy giải thích tại sao.
Lời giải:
Độ dài của cái thước là cạnh huyền của một tam giác vuông CED có hai cạnh góc vuông là EC và ED.
Ta có: ED có độ dài bằng 6 lần độ dài cạnh của một ô vuông. Nên ta có thể lấy hai điểm F, H sao cho chia đoạn ED thành ba đoạn, mỗi đoạn có độ dài bằng 2 lần độ dài cạnh của một ô vuông.
Từ F và H ta kẻ hai đường thẳng song song với cạnh EC cắt cạnh CDlần lượt tại G và I.
Theo định lí Thalès, ta chứng minh được DI = IG = GC (cùng bằng \(\dfrac{1}{3}CD\))
Vậy ta có thể chia được cái thước thành ba phần bằng nhau mà không sử dụng thước đo.
II. Ước lượng chiều cao
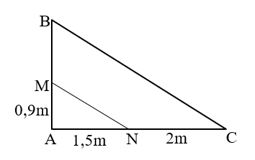
Luyện tập 2 trang 60 Toán 8 Tập 2: Người ta đo bóng của một cây và được các số đo ở Hình 23. Giả sử rằng các tia nắng song song với nhau, hãy tính độ cao x.
Lời giải:
Đoạn thẳng AB biểu thị cho độ cao của cây, đoạn thẳng AM và MB lần lượt biểu thị độ cao của thân và tán cây, đoạn thẳng AN và NC lần lượt biểu thị độ dài cái bóng của thân cây và tán cây, đoạn thẳng MN và BC lần lượt biểu thị cho các tia nắng.
Xét ∆ABC với MN // BC, ta có: \(\dfrac{AM}{MB} = \dfrac{AN}{NB}\) (định lí Thalès)
Suy ra \(\dfrac{0,9}{x} = \dfrac{1,5}{2}\)
Do đó \(x = \dfrac{0,9.2}{1,5} = 1,2\)
Vậy độ cao x = 1,2 m.
Bài tập
Bài 1 trang 60 Toán 8 Tập 2: Để đo khoảng cách giữa hai vị trí A và B trong đó B không tới được, người ta tiến hành chọn các vị trí C, D, E như ở Hình 24 và đo được AC = 50m, CD = 20m, DE = 18m. Hỏi khoảng cách giữa hai vị trí A và B là bao nhiêu?
Lời giải:
Do DE ⊥ AC, AB ⊥ AC nên DE // AB.
Xét ∆ABC với DE // AB, ta có:
\(\dfrac{CD}{CA} = \dfrac{DE}{AB}\)
(hệ quả của định lí Thalès)Suy ra \(\dfrac{20}{50} = \dfrac{18}{AB}\)
Vậy khoảng cách giữa hai vị trí A và B là 45 m.
Bài 2 trang 61 Toán 8 Tập 2: Có thể gián tiếp đo chiều cao của một bức tuờng khá cao bằng dụng cụ đơn giản được không?
Hình 25 thể hiện cách đo chiều cao AB của một bức tường bằng các dụng cụ đơn giản gồm: hai cọc thẳng đứng (cọc 1 cố định; cọc 2 có thể di động được) và sợi dây FC. Cọc 1 có chiều cao DK = h. Các khoảng cách BC = a, DC = b đo được bằng thước dây thông dụng.
a) Em hãy cho biết người ta tiến hành đo đạc như thế nào?
b) Tính chiều cao AB theo h, a, b.
Lời giải:
a) Cách tiến hành:
- Vì cọc 2 di động được nên di chuyển cọc 2 sao cho cọc 2 trùng với AB, cụ thể F trùng với A, E trùng với B.
- Lúc này cọc 1 song song với AB. Do đó, ta có tỉ lệ giữa chiều cao của cọc 1 và AB bằng với tỉ lệ giữa khoảng cách DC và BC. Từ đó ta tính được chiều cao AB của bức tường thông qua hệ quả của định lí Thalès.
b) Xét ∆ABC với AB // KD (D ∈ BC, K ∈ AC), ta có:
\(\dfrac{DK}{BA} = \dfrac{DC}{BC}\)(hệ quả định lí Thalès)
Suy ra \(AB = \dfrac{DK.BC}{DC} = \dfrac{h.a}{b}\)
Vậy chiều cao \(AB = \dfrac{h.a}{b}\)
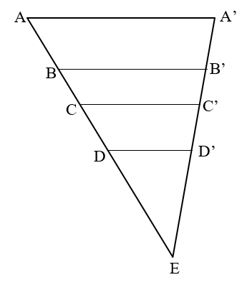
Bài 3 trang 61 Toán 8 Tập 2: Trong Hình 26, các thanh AA’, BB’, CC’, DD’ của giàn gỗ song song với nhau. Không sử dụng thước đo, hãy giải thích vì sao độ dài các đoạn AB, BC, CD lần lượt tỉ lệ với độ dài các đoạn A’B’, B’C’, C’D’.
Lời giải:
Xét ∆ECC’với DD’ // CC’, ta có: \(\dfrac{ED}{DC} = \dfrac{ED'}{D'C'}\) (định lí Thalès)
Suy ra \(\dfrac{ED}{ED'} = \dfrac{ED'}{D'C'}\) (1)
Xét ∆EBB’với DD’ // BB’, ta có: \(\dfrac{ED}{DB} = \dfrac{ED'}{D'B'}\) (định lí Thalès)
Suy ra \(\dfrac{ED}{ED'} = \dfrac{DB}{D'B'}\) (2)
Từ (1) và(2) ta có \(\dfrac{DC}{D'C'} = \dfrac{DB}{D'B'} = \dfrac{DB - DC}{D'B' - D'C'} = \dfrac{BC}{B'C'}\) (4)
Xét ∆EAA’với DD’ // AA’, ta có: \(\dfrac{ED}{DA} = \dfrac{ED'}{D'A'}\) (định lí Thalès)
Suy ra \(\dfrac{ED}{ED'} = \dfrac{DA}{D'A'}\) (3)
Từ (2) và (3) ta có \(\dfrac{DB}{D'B'} = \dfrac{DA}{D'A'} = \dfrac{DA - DB}{D'A' - D'B'} = \dfrac{AB}{A'B'}\) (5)
Từ (4) và (5) ta có \(\dfrac{AB}{A'B'} = \dfrac{BC}{B'C'} = \dfrac{CD}{C'D'}\)
Bài 4 trang 61 Toán 8 Tập 2: Anh Thiện và chị Lương đứng ở hai phía bờ sông và muốn ước lượng khoảng cách giữa hai vị trí A, B ở hai bên bờ sông (Hình 27).
- Anh Thiện chọn vị trí Cở trên bờ sông sao cho A, B, C thẳng hàng và đo được BC = 4m;
- Tiếp theo, anh Thiện xác định vị trí D, chị Lương xác định vị trí E sao cho D, B, E thẳng hàng, đồng thời \(\widehat{BAE} = \widehat{BCD} = 90°\)
- Anh Thiện đo được CD = 2m, chị Lương đo được AE = 12m.
Hãy tính khoảng cách giữa hai vị trí A và B.
Lời giải:
Ta có: AE ⊥ AC, CD ⊥ AC nên AE // CD.
Xét ∆ABE với AE // CD, ta có: \(\dfrac{AB}{BC} = \dfrac{AE}{CD}\) (hệ quả của định lí Thalès)
Suy ra \(\dfrac{AB}{4} = \dfrac{12}{2}\)
Do đó \(AB = \dfrac{12.4}{2} = 24\)
Vậy khoảng cách AB là 24 m.
-//-
Hy vọng với nội dung trả lời chi tiết câu hỏi trong Bài 2: Ứng dụng của định lí Thalès trong tam giác giúp học sinh nắm được nội dung bài học và ghi nhớ những nội dung chính, quan trọng trong chương trình học Toán học 8.