Hướng dẫn trả lời câu hỏi và giải bài tập Toán 8 Cánh Diều tập 2 giúp học sinh nắm được các cách giải bài tập Chương 8: Tam giác đồng dạng. Hình đồng dạng chuẩn bị bài trước khi tới lớp và luyện tập giải toán tại nhà.
Chương 8 Bài 1: Định lí Thalès trong tam giác
Khởi động trang 52 Toán 8 Tập 2: Bác Dư muốn cắt một thanh sắt (Hình 1) thành 5 phần bằng nhau nhưng bác lại không có thước để đo.
Bác Dư có thể thực hiện điều đó bằng cách nào?
Lời giải:
Sau bài học này, chúng ta có thể giải quyết câu hỏi trên như sau:
Bác Dư có thể làm như sau:
– Đặt thanh sắt trên mặt phẳng sân và coi thanh sắt như đoạn thẳng AB.
– Vẽ tia Ax và lấy một đoạn dây không dãn nào đó rồi đặt liên tiếp trên tia Ax, bắt đầu từ điểm A, năm đoạn thẳng AM, MN, NP, PQ, QC có độ dài đều bằng độ dài đoạn dây.
– Trong tam giác ABC, kẻ đường thẳng qua M song song với cạnh BC, cắt cạnh AB tại I.
Theo định lí Thalès, ta có \(\dfrac{AI}{AB} = \dfrac{AM}{AC} = \dfrac{1}{5}\). Do đó \(AI = \dfrac{1}{5}AB\).
Dựa theo đoạn mẫu AI, bác Dư có thể cắt một thanh sắt thành năm phần bằng nhau.
I. Đoạn thẳng tỷ lệ
Hoạt động 1 trang 52 Toán 8 Tập 2: Cho hai đoạn thẳng AB = 2 cm, CD = 3 cm và hai đoạn thẳng MN = 4 cm, PQ = 6 cm. So sánh hai tỉ số \(\dfrac{AB}{CD}, \dfrac{MN}{PQ}\)
Lời giải:
Ta có:\( \dfrac{AB}{CD} = \dfrac{2}{3}\) và \(\dfrac{MN}{PQ} = \dfrac{4}{6} = \dfrac{2}{3}\)
Vậy \(\dfrac{AB}{CD} = \dfrac{MN}{PQ} = \dfrac{2}{3}\)
II. Định lí Thalès trong tam giác
Hoạt động 2 trang 53 Toán 8 Tập 2: Quan sát Hình 3 và cho biết:
a) Đường thẳng d có song song với BC hay không;
b) Bằng cách đếm số ô vuông, dự đoán xem các tỉ số \(\dfrac{AM}{MB}, \dfrac{AN}{NC}\) có bằng nhau hay không.
Lời giải:
a) Đường thẳng dvà BC nằm trên hai dòng kẻ nên đường thẳng d song song với BC;
b) Ta có \(\dfrac{AM}{MB} = \dfrac{2}{1} = 2\) và \(\dfrac{AN}{NC} = \dfrac{2}{1} = 2\)
Vậy \(\dfrac{AM}{MB} = \dfrac{AN}{NC} = 2\)
Luyện tập 1 trang 53 Toán 8 Tập 2: Trong Hình 4, chứng tỏ rằng nếu MN // BC thì \(\dfrac{MB}{AB} = \dfrac{NC}{AC}\)
Lời giải:
Do MN // BC nên theo định lí Thalès, ta có: \(\dfrac{AM}{MB} = \dfrac{AN}{NC}\)
Suy ra \(\dfrac{AM}{AN} = \dfrac{MB}{NC}\) (tính chất tỉ lệ thức)
Do đó \(\dfrac{AM}{AN} = \dfrac{MB}{NC} = \dfrac{AM + MB}{AN+NC} = \dfrac{AB}{AC}\) (tính chất dãy tỉ số bằng nhau)
Hay \(\dfrac{MB}{NC} = \dfrac{AB}{AC}\), nên \(\dfrac{MB}{AB} = \dfrac{NC}{AC}\)
Luyện tập 2 trang 53 Toán 8 Tập 2: Cho tam giác ABC có G là trọng tâm. Đường thẳng qua G song song với BC lần lượt cắt cạnh AB, AC tại M, N. Chứng minh \(\dfrac{AM}{AB} = \dfrac{AN}{AC} = \dfrac{2}{3}\)
Lời giải
Tương tự, xét xét ∆ABC với MN // BC ta cũng có \(\dfrac{AM}{AB} = \dfrac{AN}{AC}\) (2)
Từ (1) và (2), suy ra \(\dfrac{AM}{AB} = \dfrac{AN}{AC} = \dfrac{2}{3}\)
Hoạt động 3 trang 54 Toán 8 Tập 2: Trong Hình 7, cho AM = 1, MB = 2, AN = 1,5, NC = 3.
a) So sánh các tỉ số \(\dfrac{AM}{MB}, \dfrac{AN}{NC}\)
b) Đường thẳng d (đi qua M, N ) có song song với BC hay không?
Lời giải
Luyện tập 3 trang 55 Toán 8 Tập 2: Cho tam giác ABC vuông tại A có CA = 4, CB = 5. Giả sử M, N là hai điểm lần lượt nằm trên hai cạnh CA, CB sao cho CM = 1, CN = 1,25. Tính độ dài đoạn thẳng MN.
Lời giải
Bài tập
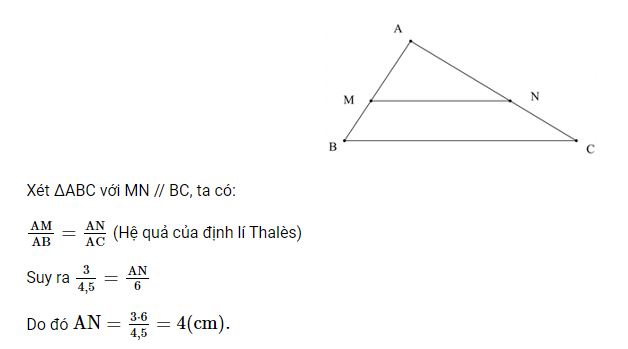
Bài 1 trang 57 Toán 8 Tập 2: Cho tam giác ABC có AB = 4,5 cm; AC = 6 cm. Các điểm M, N lần lượt thuộc các cạnh AB, AC thoả mãn AM = 3 cm và MN // BC. Tính độ dài đoạn thẳng AN.
Lời giải:
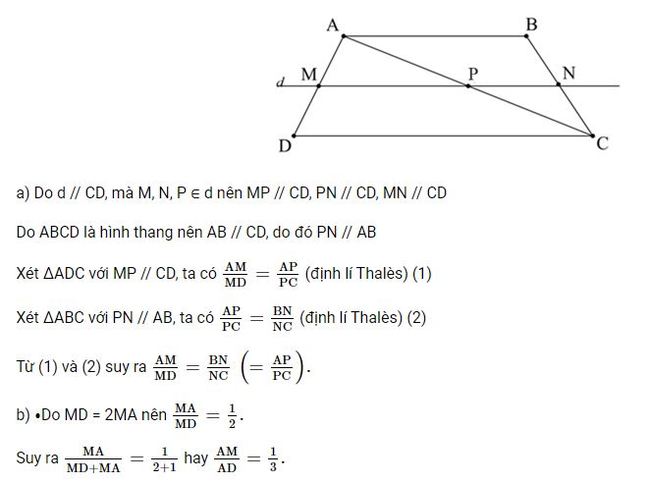
Bài 2 trang 57 Toán 8 Tập 2: Cho hình thang ABCD (AB // CD) có AB = 4 cm, CD = 6 cm. Đường thẳng d song song với hai đáy và cắt hai cạnh bên AD, BC của hình thang đó lần lượt tại M, N; cắt đường chéo AC tại P.
a) Chứng minh \(\dfrac{AM}{MD} = \dfrac{BN}{NC}\)
b) Tính độ dài các đoạn thẳng MP, PN, MN; biết rằng MD = 2MA.
Lời giải:
Bài 3 trang 57 Toán 8 Tập 2: Trong Hình 15, cho MN // AB, NP // BC. Chứng minh MP // AC.
Lời giải:
Bài 4 trang 57 Toán 8 Tập 2: Trong Hình 16, độ dài đoạn thẳng A’C’ mô tả chiều cao của một cái cây, đoạn thẳng AC mô tả chiều cao của một cái cọc (cây và cọc cùng vuông góc với đường thẳng đi qua ba điểm A’, A, B). Giả sử AC = 2m, AB = 1,5m, A’B = 4,5 m. Tính chiều cao của cây.
Lời giải:
Ta có: AC ⊥ A’B, A’C’ ⊥ A’B nên AC // A’C’
Xét ∆A’BC’ với AC // A’C’, ta có: \(\dfrac{AC}{A'C'} = \dfrac{BA}{BA'}\) (hệ quả định lí Thalès)
Suy ra \(\dfrac{AC}{A'C'} = \dfrac{1,5}{4,5} = \dfrac{1}{3}\)
Suy ra A’C’ = 3AC = 3.2 = 6 (m).
Vậy cây cao 6m.
Bài 5 trang 57 Toán 8 Tập 2: Cho đoạn thẳng AB. Hãy trình bày cách chia đoạn thẳng AB thành ba đoạn thẳng bằng nhau mà không dùng thước để đo.
Lời giải:
-//-
Hy vọng với nội dung trả lời chi tiết câu hỏi trong Bài 1: Định lí Thalès trong tam giác giúp học sinh nắm được nội dung bài học và ghi nhớ những nội dung chính, quan trọng trong chương trình học Toán học 8.