Giải bài tập 70 trang 88 sách giáo khoa Toán 7 tập 2 - Hình học

Đề bài

Cho A, B là hai điểm phân biệt và d là đường trung trực của đoạn thẳng AB.

a) Ta kí hiệu 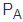 là nửa mặt phẳng bờ d có chứa điểm A (không kể đường thẳng d). Gọi N là một điểm của  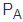và N là giao điểm của đường thẳng NB và d. Hãy so sánh NB với NM + MA; từ đó suy ra NA < NB.

b) Ta kí hiệu 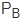 là nửa mặt phẳng bờ d có chứa điểm B (không kể điểm d). Gọi N’ là một điểm của 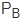. Chứng minh rằng N’B < N’A.

c) Gọi L là một điểm sao cho LA < LB. Hỏi điểm L nằm ở đâu, trong 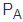,  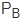hay trên d?

Phương pháp

- Áp dụng tính chất đường trung trực của đoạn thẳng.

- Áp dụng bất đẳng thức trong tam giác.

Hướng dẫn giải

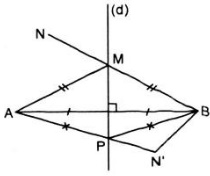
a) - Ta có M nằm trên đường trung trực của AB nên MA = MB.

Vì M nằm giữa đoạn NB nên:

    NB = NM + MB hay NB = NM + MA (vì MB = MA)

Vậy NB = NM + MA

- Trong ΔNMA có: NA < NM + MA

Vì NM + MA = NB nên NA < NB (đpcm).

b) Nối N'A cắt (d) tại P. Vì P nằm trên đường trung trực của đoạn AB nên: PA = PB

Ta có: N'A = N'P + PA = N'P + PB

Trong ΔN'PB ta có: N'B < N'P + PB

Do đó: N'B < N'A (đpcm)

c) - Vì LA < LB nên L không thuộc đường trung trực d.

- Từ câu b) ta suy ra với điểm N' bất kì thuộc PB thì ta có N'B < N'A. Do đó, để LA < LB thì L không thuộc .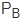

- Từ câu a) ta suy ra với điểm N bất kì thuộc PA thì ta có NA < NB. Do đó, để LA < LB thì L thuộc .