Bài 59 trang 90 SGK Toán 9 tập 2

Những nội dung dưới đây không chỉ giúp bạn biết được cách làm, tham khảo đáp án bài 59 trang 90 SGK Toán 9 tập 2 mà còn hỗ trợ bạn ôn tập để nắm vững các kiến thức chương 3 phần hình học Toán 9 đã được học trên lớp về tứ giác nội tiếp.

Đề bài 59 trang 90 SGK Toán 9 tập 2

Cho hình bình hành \(ABCD.\) Đường tròn đi qua ba đỉnh \(A, \, B, \, C\) cắt đường thẳng \(CD\) tại \(P\) khác \(C.\) Chứng minh \(AP = AD.\)

» Bài tập trước: Bài 58 trang 90 SGK Toán 9 tập 2

Giải bài 59 trang 90 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Số đo tổng hai góc đối diện của tứ giác nội tiếp bằng \(180^0.\)

+) Sử dụng tính chất hai đường thẳng song song, tính chất hình bình hành.

Đáp án chi tiết

Dưới đây là các cách giải bài 59 trang 90 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

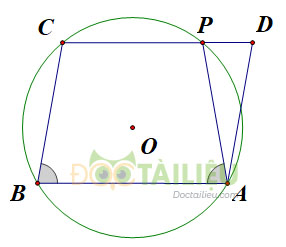
Do tứ giác \(ABCP\) nội tiếp nên ta có:

\(\widehat{BAP} + \widehat{BCP} = 180^0.\)        (1)

Ta lại có: \(\widehat{ABC}+ \widehat{BCP}=  180^0\) (hai góc trong cùng phía do \(CD//AB\)).      (2)

Từ (1) và (2) suy ra: \(\widehat{BAP}= \widehat{ABC}.\)

Vậy \(ABCP\) là hình thang cân, suy ra \(AP = BC.\)      (3)

Mà \(BC = AD\) (hai cạnh đối của hình bình hành)  (4)

Từ (3) và (4) suy ra \(AP = AD\) (đpcm).

» Bài tiếp theo: Bài 60 trang 90 SGK Toán 9 tập 2

Trên đây là nội dung hướng dẫn trả lời bài 59 trang 90 SGK Toán 9 tập 2 được Đọc Tài Liệu chia sẻ để giúp bạn hoàn thành tốt bài làm của mình. Mong rằng những tài liệu giải Toán 9 của chúng tôi sẽ luôn là người bạn đồng hành để giúp bạn học tốt hơn môn học này.