Bài 58 trang 90 SGK Toán 9 tập 2

Bạn muốn giải bài 58 trang 90 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết, không chỉ tham khảo cách làm hoặc đáp án mà bài viết này còn giúp bạn nắm vững lại các kiến thức Toán 9 chương 3 phần hình học để tự tin giải tốt các bài tập khác về tứ giác nội tiếp.

Đề bài 58 trang 90 SGK Toán 9 tập 2

Cho tam giác đều \(ABC.\) Trên nửa mặt phẳng bờ \(BC\) không chứa đỉnh \(A,\) lấy điểm \(D\) sao cho \(DB = DC\) và \(\widehat{DCB}=\dfrac{1}{2}\widehat{ACB}.\)

a) Chứng minh \(ABDC\) là tứ giác nội tiếp.

b) Xác định tâm của đường tròn đi qua bốn điểm \(A,\, B,\, D, \,C\).

» Bài tập trước: Bài 57 trang 89 SGK Toán 9 tập 2

Giải bài 58 trang 90 SGK Toán 9 tập 2

Hướng dẫn cách làm

a ) +) Tứ giác có tổng hai góc đối diện bằng \(180^0\) thì tứ giác đó là tứ giác nội tiếp.

+) Sử dụng tính chất tam giác đều, tính chất tam giác cân

b) Trong tam giác vuông, tâm đường tròn ngoại tiếp là trung điểm cạnh huyền

Đáp án chi tiết

Dưới đây là các cách giải bài 58 trang 90 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

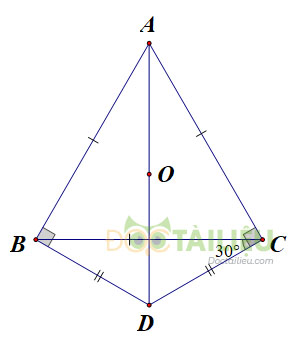
a) Theo giả thiết, \(\widehat{DCB}=\frac{1}{2}\widehat{ACB} = \dfrac{1}{2} .60^0= 30^0.\)

\(\widehat{ACD}=\widehat{ACB} +\widehat{BCD}\)  (tia \(CB\) nằm giữa hai tia \(CA,\, CD\))

\(\Rightarrow\)

Do \(DB = CD\) nên \(∆BDC\) cân tại \(D\) \(\Rightarrow \widehat{DBC} = \widehat{DCB} = 30^0\)

Từ đó \(\widehat{ABD}= 30^0+60^0=90^0\) (2)

Từ (1) và (2) có \(\widehat{ACD}+ \widehat{ABD}=180^0\) nên tứ giác \(ABDC\) là tứ giác nội tiếp.

b) Vì \(\widehat{ABD}  = 90^0\) nên \(AD\) là đường kính của đường tròn ngoại tiếp tứ giác \(ABDC,\) do đó tâm đường tròn ngoại tiếp tứ giác \(ABDC\) là trung điểm \(AD.\)

» Bài tiếp theo: Bài 59 trang 90 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 58 trang 90 Toán hình học 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.