Giải bài tập 55 trang 80 sách giáo khoa Toán 7 tập 2 - Hình học

Đề bài

Cho hình 51: Chứng minh ba điểm B, C, D thẳng hàng.

Gợi ý: Chứng minh góc ADB + góc ADC = 180⁰

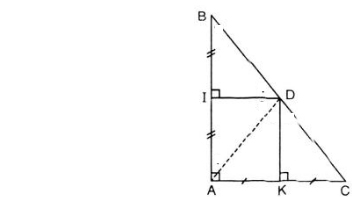
Hướng dẫn giải

Nối BD và CD.

Từ hình vẽ ta có DK là đường trung trực của AC, DI là đường trung trực của AB nên:

BD = AD = CD

Xét ΔADK và ΔCDK có:

AD = CD

DK chung

AK = KC

=> ΔADK = ΔCDK (c.c.c)

=> Góc ADK = góc CDK

hay DK là tia phân giác của góc ADC

=> ADK = 1/2 góc ADC

Tương tự ∆ADI = ∆BDI (c.c.c)

=> Góc ADI = góc BDI

=> DI là tia phân giác của góc ADB

=> Góc ADI = 1/2 góc ADB

Vì AC // DI ( cùng vuông góc với AB) mà DK ⊥ AC

⇒ DK ⊥ DI

hay góc ADK + góc ADI = 90⁰

Do đó 1/2 góc ADC + 1/2 góc ADB = 90⁰

=> góc ADC + góc ADB = 180⁰

Vậy B, D, C thẳng hàng (đpcm).