Bài 50 trang 87 SGK Toán 9 tập 2

Bạn muốn giải bài 50 trang 87 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết, không chỉ tham khảo cách làm hoặc đáp án mà bài viết này còn giúp bạn nắm vững lại các kiến thức Toán 9 chương 3 phần hình học để tự tin giải tốt các bài tập khác về cung chứa góc.

Đề bài 50 trang 87 SGK Toán 9 tập 2

Cho đường tròn đường kính \(AB\) cố định. \(M\) là một điểm chạy trên đường tròn. Trên tia đối của tia \(MA\) lấy điểm \(I\) sao cho \(MI = 2MB.\)

a) Chứng minh \(\widehat{AIB}\) không đổi.

b) Tìm tập hợp các điểm \(I\) nói trên.

» Bài tập trước: Bài 49 trang 87 SGK Toán 9 tập 2

Giải bài 50 trang 87 SGK Toán 9 tập 2

Hướng dẫn cách làm

a) Sử dụng góc nội tiếp chắn nửa đường tròn là góc vuông và tỉ số lượng giác của góc nhọn

b) Chứng minh theo hai phần: Phần thuận và phần đảo.

Lập luận để có quỹ tích là cung chứa góc \(AIB\) dựng trên đoạn BC.

Chú ý đến giới hạn của quỹ tích.

Đáp án chi tiết

Dưới đây là các cách giải bài 50 trang 87 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

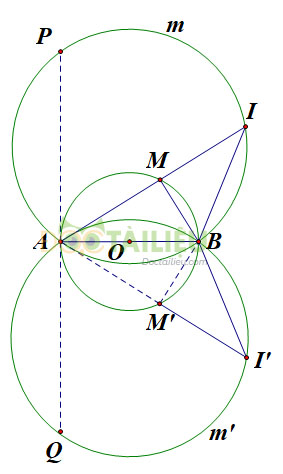
a) Gọi \(O\) là trung điểm \(AB\). Xét đường tròn tâm \(O\) có \(\widehat {AMB}\)  là góc nội tiếp chắn nửa đường tròn nên \(\widehat {AMB} = 90^\circ \)  hay \(AM \bot MB\)

Xét tam giác vuông \(MBI\) có \(MI = 2MB \Rightarrow \tan \widehat {MIB} = \dfrac{{MB}}{{MI}} = \dfrac{{MB}}{{2MB}} = \dfrac{1}{2}\)

Suy ra \(\widehat {AIB} = \alpha \) không đổi và thỏa mãn \(\tan \alpha  = \dfrac{1}{2}.\)

b) Phần thuận:

Khi điểm M thay đổi trên đường tròn đường kính AB thì điểm I thay đổi và luôn nhìn cạnh AB dưới một góc \(\widehat {AIB} = \alpha \) không đổi (với \(\tan \alpha  = \dfrac{1}{2}\))

Vậy điểm I thuộc hai cung chứa góc \(\alpha \) sao cho \(\tan \alpha  = \dfrac{1}{2}\) dựng trên đoạn AB.

Nhưng tiếp tuyến PQ với đường tròn đường kính AB tại A là vị trí giới hạn của AM. Do đó điểm I thuộc hai cung \(PmB,Qm'B\).

Hai điểm P, Q là các điểm giới hạn của quỹ tích, điểm B là điểm đặc biệt của quỹ tích

Phần đảo:

Lấy điểm \(I'\) bất kỳ thuộc cung \(Qm'B\) (hoặc cung \(PmB\)). Nối \(AI'\) cắt đường tròn tâm \(O\) tại \(M'.\) Ta chứng minh \(M'I' = 2M'B.\)

Xét \(\left( O \right)\) có \(\widehat {AM'B}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat {AM'B} = 90^\circ  \Rightarrow AM' \bot BM' \Rightarrow \widehat {BM'I'} = 90^\circ \)

Xét tam giác \(BM'I'\) vuông ở \(M'\) có \(\widehat {BI'M'} = \alpha \) (do \(I'\) bất kỳ thuộc cung \(Qm'B\) là cung chứa góc \(\alpha \) dựng trên đoạn AB) nên \(\tan \widehat {BI'M'} = \tan \alpha  = \dfrac{1}{2}\) mà \(\tan \widehat {BI'M'} = \dfrac{{BM'}}{{M'I'}} \Rightarrow \dfrac{{BM'}}{{M'I'}} = \dfrac{1}{2} \Rightarrow M'I' = 2BM'\)

Kết luận: Quỹ tích các điểm I là hai cung \(PmB,Qm'B\).

» Bài tiếp theo: Bài 51 trang 87 SGK Toán 9 tập 2

Nội dung trên đã giúp bạn nắm được cách làm bài 50 trang 87 SGK Toán 9 tập 2. Hy vọng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ giúp các bạn hoàn thành bài tập chính xác và học tốt môn học này.