Bài 47 trang 86 SGK Toán 9 tập 2

Để giải bài 47 trang 86 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết về cách làm bài, Đọc Tài Liệu sẽ giúp các bạn đưa ra đáp án chính xác nhất và ôn tập các kiến thức trong chương trình học Toán 9 chương 3 phần hình học về cung chứa góc.

Đề bài 47 trang 86 SGK Toán 9 tập 2

Gọi cung chứa góc \(55^0\) ở bài tập 46 là \(\overparen{AmB}\). Lấy điểm \({M_1}\) nằm bên trong và điểm \({M_2}\) nằm bên ngoài đường tròn chứa cung này sao cho \({M_1},{M_2}\) và cung \(\overparen{AmB}\) nằm cùng về một phía đối với đường thẳng \(AB\). Chứng minh rằng:

a) \(\widehat {A{M_1}B} > 55^0\);

b) \(\widehat {A{M_2}B} < 55^0\). 

» Bài tập trước: Bài 46 trang 86 SGK Toán 9 tập 2

Giải bài 47 trang 86 SGK Toán 9 tập 2

Hướng dẫn cách làm

 Sử dụng:

+ Số đo của góc có đỉnh bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn

+ Số đo của góc có đỉnh bên trong đường tròn bằng nửa hiệu số đo hai cung bị chắn 

Đáp án chi tiết

Dưới đây là các cách giải bài 47 trang 86 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

a) \({M_1}\) là điểm bất kì nằm trong cung chứa góc \(55^0\) (hình vẽ).

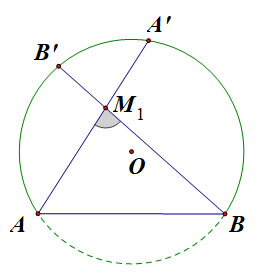
Gọi \(A', \,  B’\) theo thứ tự là giao điểm của \({M_1}A,\)  \({M_1}B\) với cung tròn.

Ta có \(\widehat {AA'B} = \dfrac{1}{2}\) sđ \(\overparen{AB} = 55^\circ \) (góc nội tiếp chắn cung \(AB\) và cung \(AmB\) là cung chứa góc \(55^\circ \))

Vì \(\widehat{A{M_1}B}\) là góc có đỉnh nằm trong đường tròn chắn cung \(A'B'\) và \(AB\) nên:  

\(\widehat {A{M_1}B}\) \(=\dfrac{sđ\overparen{AB}+sđ\overparen{A'B'}}{2}>\dfrac {1}{2}sđ\overparen{AB} =55^0\).

Vậy \(\widehat {A{M_1}B} > 55^0\) 

b)  \({M_2}\) là điểm bất kì nằm ngoài đường tròn (hình vẽ ) 

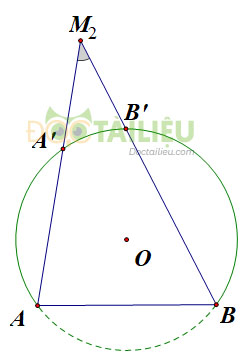
Ta có \({M_2}A, \, {M_2}B\) lần lượt cắt đường tròn tại \(A’, \, B’.\)

\(\widehat {AA'B} = \dfrac{1}{2}\) sđ \(AB = 55^\circ \) (góc nội tiếp chắn cung \(AB\) và cung \(AmB\) là cung chứa góc \(55^\circ \))

Vì góc \(\widehat {A{M_2}B}\) là góc có đỉnh nằm bên ngoài đường tròn chắn cung \(A'B'\) và \(AB\) nên:

\(\widehat {A{M_2}B}= \dfrac{sđ\overparen{AB}-sđ\overparen{A'B'}}{2}<\dfrac {1}{2}sđ\overparen{AB} =55^0 .\)

Vậy  \(\widehat {A{M_2}B} < 55^0.\)

» Bài tiếp theo: Bài 48 trang 87 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 47 trang 86 Toán hình học 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.