Giải bài tập 41 trang 73 sách giáo khoa Toán 7 tập 2 - Hình học

Đề bài

Hỏi trọng tâm của một tam giác đều có cách đều ba cạnh của nó hay không? Vì sao?

Phương pháp

Áp dụng tính chất ba đường trung tuyến của tam giác.

Hướng dẫn giải

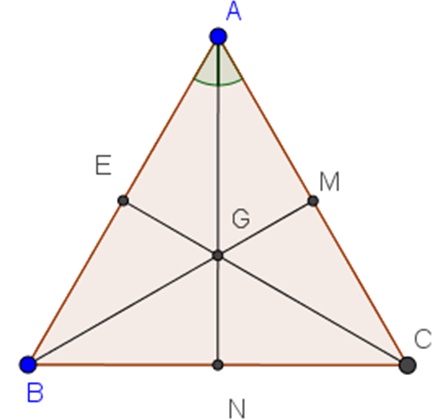
Giả sử ta có ΔABC đều và có trọng tâm G.

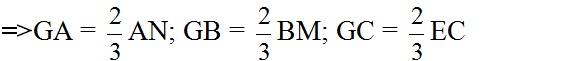
Vì ΔABC đều nên ba trung tuyến AN, BM, CE bằng nhau

Suy ra: GA = GB = GC

Do đó: ΔAMG = ΔCMG (c.c.c)

=> góc AMG = góc CMG

Mà góc AMG + góc CMG = 180⁰

=> góc AMG = 90⁰

=> GM ⊥ AC tức là GM là khoảng cách từ G đến AC.

Chứng minh tương tự GE, GN là khoảng cách từ G đến AB, BC.

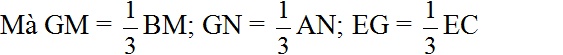
Và AN = BM = EC nên GM = GN = GE

Hay G cách đều ba cạnh của tam giác ABC.