Giải bài tập 39 trang 73 sách giáo khoa Toán 7 tập 2 - Hình học

Đề bài

Cho hình 39.

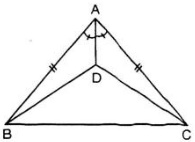
a) Chứng minh ∆ABD = ∆ACD.

b) So sánh góc DBC với góc DCB.

Phương pháp

- Chứng minh  ∆ABD = ∆ACD theo trường hợp bằng nhau thứ hai của tam giác.

- Chứng minh tam giác BDC là tam giác cân, từ đó suy ra góc DBC = góc DCB

Hướng dẫn giải

a) Xét ∆ABD và ∆ACD ta có:

AB = AC

Góc BAD = góc CAD

AD là cạnh chung

Vậy ∆ABD = ∆ACD (c.g.c) (đpcm).

b)  Vì ∆ABD = ∆ACD (cmt)

⇒ BD = CD

⇒  ∆BCD cân tại D

⇒ góc DBC = góc DCB (đpcm)