Đáp án bài 3 trang 60 sách giáo khoa hình học lớp 11

1. Đề bài

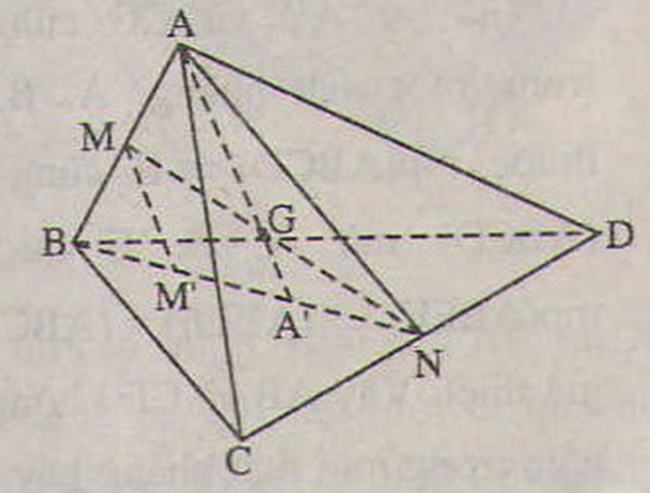
Cho tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB, CD và G là trung điểm của đoạn MN.

• a) Tìm giao điểm A’ của đường thẳng AG và mp(BCD).
• b) Qua M kẻ đường thẳng Mx song song với AA’ và Mx cắt (BCD) tại M’.
• c) Chứng minh GA = 3GA’

2. Đáp án - hướng dẫn

a) Trong (ABN) : Gọi A′ = AG ∩ BN suy ra A′ ∈ BN , BN ⊂ (BCD) .

Do đó: A′ ∈ (BCD) => A′ = AG ∩ (BCD) .

b) MM′ / / AA′ mà AA′ ⊂ (ABA′) do đó: MM′ ⊂ (ABA′)

Mặt khác M′ ∈ (BCD) nên M′ thuộc giao tuyến A′B của (ABA′) và (DBC)

*) Xét tam giác NMM′ có:

+) G là trung điểm của NM .

+) GA′ // MM′ ⇒ A ′ là trung điểm của NM′ Xét tam giác BAA′ có:

+) M là trung điểm của AB

+) MM′ // AA′ ⇒ M′ là trung điểm của BA′ Do đó: BM′ = M′ A′ = A′N .

c) Ta có 2GA′ =  MM′

2MM′ =  AA′ ⇒ 4GA′ =  AA′ ⇒ GA = 3 GA′