Lý thuyết tính chất đường thẳng và mặt phẳng song song

- Định lý 1

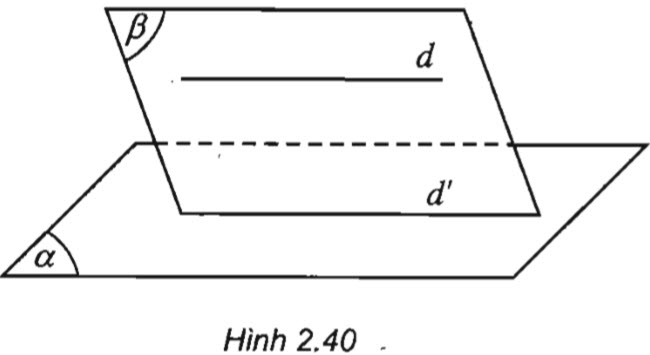
Nếu đường thẳng d không nằm trên mặt phẳng (α) và song song với một đường thẳng d' nào đó nằm trên mặt phẳng (α) thì d song song với (α)

- Định lý 2

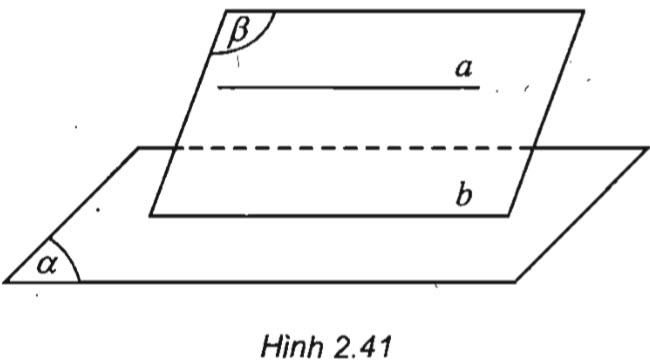
Cho đường thẳng a song song với mặt phẳng (α). Nếu mặt phẳng (β) chứa a và cắt (α) theo giao tuyến b thì b song song với a

Hệ quả 

Nếu hai mặt phẳng phân biệt cùng song song với một đường thẳng  thì giao tuyến của chúng (nếu có) cũng song song với đường thẳng đó

- Định lý 3 

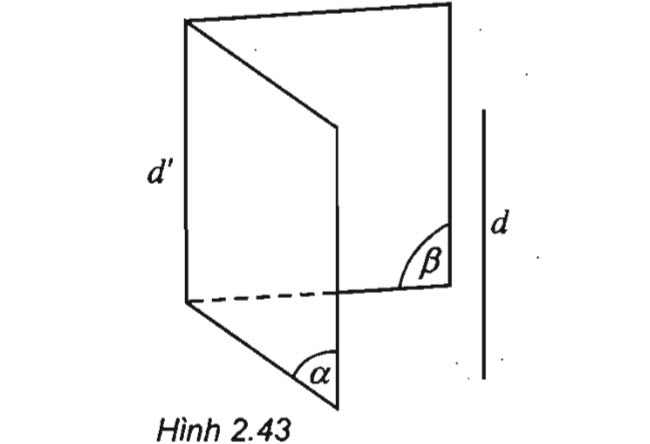
Cho hai đường thẳng chéo nhau. Có duy nhất một mặt phẳng chứa đường thẳng này và song song với đường thẳng kia