Khái niệm về phép dời hình và hai hình bằng nhau

Cùng Đọc tài liệu tìm hiểu nội dung hhái niệm về phép dời hình và hai hình bằng nhau dưới đây:

Lý thuyết

1. Khái niệm phép dời hình

a) Định nghĩa

Phép dời hình là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kỳ.

Ký hiệu: F

- Nếu F(M) = M’ và F(N) = N’ thì MN = M’N’

b) Nhận xét

- Các phép đồng nhất, tịnh tiến, đối xứng trục, đối xứng tâm, quay đều là phép dời hình.

- Phép biến hình có được bằng cách thực hiện liên tiếp hai phép dời hình cũng là một phép dời hình.

c. Tính chất của phép dời hình

Phép dời hình:

Biến ba điểm thẳng hàng thành ba điểm thẳng hàng và bảo toàn thứ tự giữa các điểm.

Biến đường thẳng thành đường thẳng, biến tia thành tia, biến đoạn thẳng thành đoạn thẳng bằng nó.

Biến tam giác thành tam giác bằng nó, biến góc thành góc bằng nó.

Biến đường tròn thành đường tròn có cùng bán kính.

2. Khái niệm về hai hình bằng nhau

Hai hình được gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.

3. Chú ý

Nếu một phép dời hình biến tam giác ABC thành tam giác A′B′C′ thì nó cũng biến trọng tâm, trực tâm, tâm các đường trọn nội tiếp, ngoại tiếp.. của tam giác ABC tương ứng thành trọng tâm, trực tâm, tâm các đường trọng nội tiếp, ngoại tiếp... của tam giác A′B′C′ .

Ví dụ minh họa

a) Cho hình vuông ABCD tâm O. Tìm ảnh của các điểm A, B, O qua phép dời hình có được bằng cách thực hiện liên tiếp hai phép \( {Q_{\left( {O{{,90}^0}} \right)}}\) và phép ĐBD.

b) Quan sát hình vẽ và cho biết \(\Delta ABC\) biến thành \(\Delta A''B''C''\) qua phép dời hình nào?

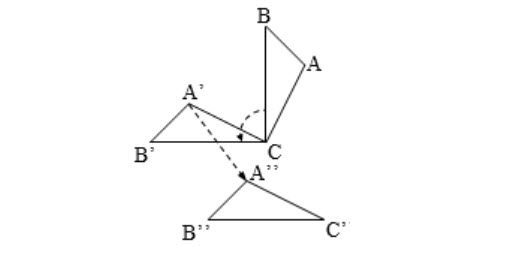
Hướng dẫn giải:

a) Ta có:

\(\left\{ \begin{array}{l}{Q_{\left( {O{{,90}^0}} \right)}}\left( O \right) = O\\{Q_{\left( {O{{,90}^0}} \right)}}\left( A \right) = B\\{Q_{\left( {O;{{90}^0}} \right)}}\left( B \right) = C\end{array} \right.\)

và ĐBD(O) = O; ĐBD(B) = B; ĐBD(C) = A.

Vậy ảnh của O là O, A là B và B là A.

b) Ta có:

\({Q_{\left( {C{{,90}^0}} \right)}}\left( {ABC} \right) = A'B'C\)

\({T_{\overrightarrow {AA''} }}\left( {A'B'C} \right) = A''B''C''.\)

Vậy phép dời hình cần tìm là phép biến hình thực hiện liên tiếp hai phép \({Q_{\left( {C{{,90}^0}} \right)}}\) và \({T_{\overrightarrow {AA''} }}.\)

Bài tập trắc nghiệm

Câu 1: 

Cho hai hình bình hành. Hãy chỉ ra một đường thẳng chia mỗi hình bình hành đó thành hai hình bằng nhau.

A. Đường thẳng đi qua hai tâm của hai hình bình hành.

B. Đường thẳng đi qua hai đỉnh của hai hình bình hành.

C. Đường thẳng đi qua tâm của hình bình hành thứ nhất và một đỉnh của hình hành còn lại.

D. Đường chéo của một trong hai hình bình hành đó.

Giải thích: Đường thẳng đi qua hai tâm của hai hình bình hành chia mỗi hình bình hành đó thành hai hình bằng nhau.

=> Đáp án: A

Câu 2: 

Cho hai đường thẳng a, b cắt nhau và góc giữa chúng là α. Gọi Đa là phép đối xứng qua a. Đb là phép đối xứng qua b. Với mọi điểm M bất kì, gọi M₁=Đa(M), M₂=Đa(M₁). Xét phép biến hình F biến M thành M₂. Trong các khẳng định sau khẳng định nào đúng?

A. F không phải là phép dời hình.

B. F là phép quay với góc quay có giá trị tuyệt đối là α

C. F là phép quay với góc quay có giá trị tuyêt đối là 2α

D. F là phép quay với góc quay 4α

Giải thích: Ta có hình vẽ:

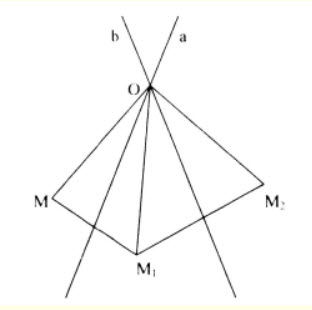
=> Đáp án: C

Câu 3: 

Cho hai điểm A, B phân biệt. Gọi ĐA là phép đối xứng qua A; T là phép tịnh tiến theo vectơ \(2\overrightarrow {AB}\) . Với điểm M bất kì, gọi M₁ = ĐA(M), M₂ =T(M₁). Gọi F là phép biến hình biến M thành M₂. Chọn khẳng định đúng.

A. F không là phép dời hình.

B. F là phép đối xứng trục.

C. F là phép đối xứng tâm.

D. F là phép tịnh tiến.

Giải thích: Ta dùng phương pháp tọa độ để giải bài toán này.

Trong mặt phẳng Oxy, gọi \(A({x_0};{y_0});B({x_1};{y_1});M(x;y) \Rightarrow {M_1}(2{x_0} - x;2{y_0} - y)\)

Lại có: \(A({x_0};{y_0});B({x_1};{y_1});M(x;y) \Rightarrow {M_1}(2{x_0} - x;2{y_0} - y)\)

nên \({M_2}(2{x_1} - x;2{y_1} - y)\).

Vậy F là phép đối xứng tâm B.

=> Đáp án: C

Đọc tài liệu - Khái niệm về phép dời hình và hai hình bằng nhau -