Bài 25 trang 119 SGK Toán 9 tập 2

Để giải bài 25 trang 119 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết về cách làm bài, Đọc Tài Liệu sẽ giúp các bạn đưa ra đáp án chính xác nhất và ôn tập các kiến thức trong chương trình học Toán 9 chương 4 phần hình học về Hình nón và Hình nón cụt.

Đề bài 25 trang 119 SGK Toán 9 tập 2

Hãy tính diện tích xung quanh của hình nón cụt biết hai bán kính đáy \(a,b\) (\(a<>) và độ dài đường sinh là \(l\) (\(a,b,l\) có cùng đơn vị đo).

» Bài tập trước: Bài 24 trang 119 SGK Toán 9 tập 2

Giải bài 25 trang 119 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Diện tích xung quanh hình nón: \(S_{xq}=\pi r l.\) với \(r\) là bán kính đáy và \(l\) là đường sinh.

+) \(S_{xq \, \, nón \, \, cụt} = S_{xq \, \, hình \, \, nón \, \, lớn } - S_{xq \, \, hình \, \, nón \, \, nhỏ}.\)

Đáp án chi tiết

Dưới đây là các cách giải bài 25 trang 119 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

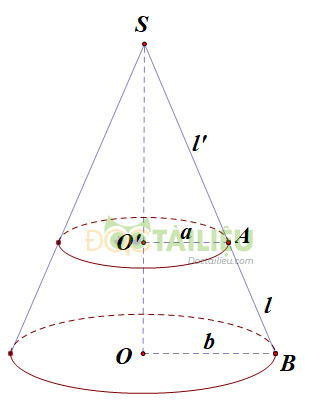
Kí hiệu như hình vẽ.  \(SA=l_1;AB=l;OB=b;O'A=a.\)

Vì  \(O'A//OB \Rightarrow \Delta SO'A \backsim \Delta SOB \Rightarrow \dfrac{{SA}}{{SB}} = \dfrac{{OA}}{{OB}}\)  \( \Leftrightarrow \dfrac{{{l_1}}}{{l + {l_1}}} = \dfrac{a}{b} \Leftrightarrow b{l_1} = al + a{l_1} \Leftrightarrow {l_1}\left( {b - a} \right) = al \Leftrightarrow {l_1} = \dfrac{a}{{b - a}}l\)

Suy ra \(SB = l + {l_1} = l + \dfrac{a}{{b - a}}l = \dfrac{b}{{b - a}}l\)

Diện tích xung quanh hình nón lớn là \({S_1} = \pi .b.SB = \pi .b.\dfrac{b}{{b - a}}l = \dfrac{{{b^2}}}{{b - a}}\pi l\)

Diện tích xung quanh hình nón nhỏ là \({S_2} = \pi .b.SA = \pi .a.\dfrac{a}{{b - a}}l = \dfrac{{{a^2}}}{{b - a}}\pi l\)

Diện tích xung quanh hình nón cụt là \(S = {S_1} - {S_2} = \dfrac{{{b^2}}}{{b - a}}\pi l - \dfrac{{{a^2}}}{{b - a}}\pi l = \pi l.\dfrac{{{b^2} - {a^2}}}{{b - a}} = \left( {a + b} \right)\pi l\)

Vậy diện tích xung quanh nón cụt là \(S = \pi \left( {a + b} \right)l\)

» Bài tiếp theo: Bài 26 trang 119 SGK Toán 9 tập 2

Nội dung trên đã giúp bạn nắm được cách làm bài 25 trang 119 SGK Toán 9 tập 2. Hy vọng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ giúp các bạn hoàn thành bài tập chính xác và học tốt môn học này.