Mời các em tham khảo tổng hợp lý thuyết Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt cùng một số dạng bài thường gặp và hướng dẫn cách làm, qua đó nắm được các định lý, công thức và áp dụng hoàn thành các bài tập.

I. Lý thuyết Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
1. Hình nón
Khi quay một tam giác vuông góc AOC một vòng quanh cạnh góc vuông OA cố định thì được một hình nón.
- Cạnh OC tạo nên đáy của hình nón, là một hình nón tâm O.
- Cạnh AC quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh, chẳng hạn AD là một đường sinh .
- A là đỉnh và AO là đường cao của hình nón.
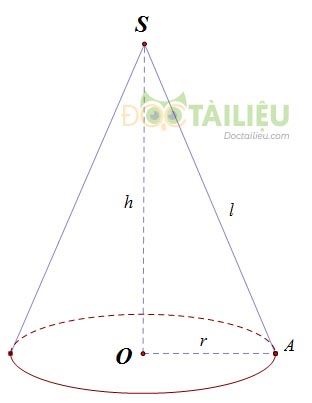
Cho hình nón có bán kính đáy R = OA, đường sinh l = SA, chiều cao h = SO. Khi đó :
+ Diện tích xung quanh: \({S_{xq}} = \pi Rl\)
+ Diện tích đáy : \({S_d} = \pi {R^2}\)
+ Diện tích toàn phần: \({S_{tp}} = {S_{xq}} + {S_d} = \pi Rl + \pi {R^2}\)
+ Thể tích: \(V = \dfrac{1}{3}\pi {R^2}h\)
+ Công thức liên hệ : \({R^2} + {h^2} = {l^2} \)
2. Hình nón cụt
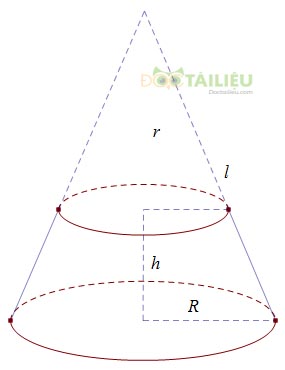
Cho hình nón cụt có các bán kính đáy là R và r,chiều cao h, đường sinh l.
+ Diện tích xung quanh: \( {S_{xq}} = \pi (R + r)l\)
+ Diện tích toàn phần: \( {S_{tp}} = \pi (R + r)l + \pi {R^2} + \pi {r^2}\)
+ Thể tích: \(V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2})\)
II. Các dạng toán thường gặp về Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Dạng 1: Tính diện tích, thể tích và các đại lượng liên quan của hình nón và hình nón cụt
Phương pháp:
Ta sử dụng các công thức ở phần lý thuyết
* Cho hình nón có bán kính đáy R = OA, đường sinh l = SA, chiều cao h = SO. Khi đó :
+ Diện tích xung quanh: \({S_{xq}} = \pi Rl\).
+ Diện tích toàn phần: \({S_{tp}} = \pi Rl + \pi {R^2}\).
+ Thể tích: \(V = \dfrac{1}{3}\pi {R^2}h\).
+ Công thức liên hệ : \({R^2} + {h^2} = {l^2}\)
* Cho hình nón cụt có các bán kính đáy là R và r,chiều cao h, đường sinh l.
+ Diện tích xung quanh: \({S_{xq}} = \pi (R + r)l.\)
+ Diện tích toàn phần: \({S_{tp}} = \pi (R + r)l + \pi {R^2} + \pi {r^2}\).
+ Thể tích: \(V = \dfrac{1}{3}\pi h({R^2} + Rr + {r^2})\).
III. Bài tập về Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Có một hình nón, bán kính đường tròn đáy là \(\displaystyle {m \over 2}(cm)\), chiều cao là 2l (cm) và một hình trụ, bán kính đường tròn đáy m (cm), chiều cao 2l (cm).
Người ta múc đầy nước vào hình nón và đổ vào hình trụ (không chứa gì cả) thì độ cao của nước trong hình trụ là:
(A) \(\displaystyle {l \over 6}(cm)\)
(B) \(l\; (cm)\)
(C) \( \displaystyle {5 \over 6} (cm)\);
(D) \(\displaystyle {{11} \over 6}l (cm)\).
Lời giải:
Thể tích hình nón là: \(\displaystyle V_1={1 \over 3}\pi {r^2}.h\)
\(\displaystyle V_1={1 \over 3}\pi {\left( {{m \over 2}} \right)^2}.2l = {1 \over 3}\pi {{{m^2}} \over 4}.2l \,\displaystyle = {{\pi {m^2}l} \over 6} (cm^3)\)
Thể tích hình trụ là: \({V_2} = \pi {r^2}.h\)
\({V_2} = \pi {m^2}.2l = 2\pi {m^2}l (cm^3)\)
\(\displaystyle {{{V_1}} \over {{V_2}}} = {{\pi {m^2}l} \over 6}:2\pi {m^2}l\,\displaystyle = {{\pi {m^2}l} \over 6}.{1 \over {2\pi {m^2}l}} \,\displaystyle = {1 \over {12}}\)
Vậy khi đổ đầy nước vào hình nón rồi đổ vào hình trụ độ cao nước là \(\displaystyle {1 \over {12}}.2l = {1 \over 6}l (cm)\)
Chọn (A).
=>> Xem thêm nhiều bài tập khác trong Toán hình 9 chương 4 bài 2 để củng cố kiến thức và rèn luyện kỹ năng làm bài
****************
Trên đây là lý thuyết Hình nón - Hình nón cụt - Diện tích xung quanh và thể tích của hình nón, hình nón cụt bao gồm các kiến thức cần nắm và những dạng bài liên quan. Hy vọng đây sẽ là tài liệu hữu ích phục vụ việc học tập của các em. Ngoài ra, các em hãy truy cập doctailieu.com để tham khảo thêm nhiều tài liệu học Toán lớp 9 phong phú khác mà chúng tôi đã sưu tầm và tổng hợp nhé. Chúc các em luôn học tốt và đạt kết quả cao!