Trong chương trình Toán lớp 9, các em sẽ được làm quen với hàm số y = ax + b. Đây là phần kiến thức quan trọng, những dạng toán về hàm số y = ax + b sẽ xuất hiện trong hầu hết các bài thi quan trọng ở các mức độ khác nhau từ dễ đến khó.
Để các em nắm được đầy đủ kiến thức về phần này, Đọc Tài Liệu đem đến tài liệu tổng hợp lý thuyết Đồ thị của hàm số y = ax + b ở bài viết dưới đây, hy vọng sẽ là một tài liệu hữu ích cho quá trình học tập của các em.
Cùng tham khảo nhé!

I. Lý thuyết Đồ thị của hàm số y = ax + b
Đồ thị hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\)
Đồ thị hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) là một đường thẳng
+ Cắt trục tung tại điểm có tung độ bằng b
+ Song song với đường thẳng y = ax nếu b \ne 0, trùng với đường thẳng y = ax nếu b = 0.
Cách vẽ đồ thị hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\)
+ Nếu \(b = 0\) ta có hàm số \(y = ax\). Đồ thị của \(y = ax\) là đường thẳng đi qua gốc tọa độ \(O(0;0)\) và điểm \(A(1;a)\).
+ Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right).\)
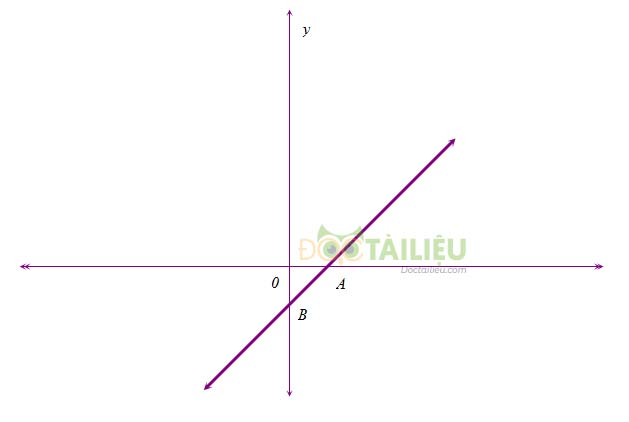
Ví dụ: Đường thẳng \(\left( d \right):y = x - 1\) đi qua điểm \(A\left( { - 1;0} \right)\) và \(B\left( {0; - 1} \right)\)
.
Lưu ý:
+ Vì đồ thị \(y = ax + b (a ≠ 0)\) là một đường thẳng nên muốn vẽ nó chỉ cần xác định hai điểm phân biệt thuộc đồ thị.
+ Trong trường hợp giá trị \(- \dfrac{b}{a}\) khó xác định trên trục \(Ox\) thì ta có thể thay điểm \(Q\) bằng cách chọn một giá trị \(x_1\) của \(x\) sao cho điểm \(Q'(x_1, y_1 )\) (trong đó \(y_1 = ax_1 + b)\) dễ xác định hơn trong mặt phẳng tọa độ.
II. Các dạng toán thường gặp Đồ thị của hàm số y = ax + b
Dạng 1: Vẽ và nhận dạng đồ thị hàm số \( y = ax + b\,\,\left( {a \ne 0} \right)\)
Phương pháp:
Đồ thị hàm số \(y = ax + b\,\,\left( {a \ne 0} \right)\) là một đường thẳng
Trường hợp 1: Nếu \( b = 0\) ta có hàm số \(y = ax.\) Đồ thị của \(y = ax \) là đường thẳng đi qua gốc tọa độ \(O(0;0)\) và điểm \(A(1;a).\)
Trường hợp 2: Nếu \(b \ne 0\) thì đồ thị \(y = ax + b\) là đường thẳng đi qua các điểm \(A(0;b),\,\,B\left( { - \dfrac{b}{a};0} \right)\).
Dạng 2: Tìm tọa độ giao điểm của hai đường thẳng
Phương pháp:
Bước 1. Xét phương trình hoành độ giao điểm của hai đường thẳng đó để tìm hoành độ giao điểm.
Bước 2. Thay hoành độ giao điểm vừa tìm được vào một trong hai phương trình đường thẳng ta tìm được tung độ giao điểm.
Dạng 3: Xác định hệ số \(a,b\) để đồ thị hàm số \(y = ax + b\,(a \ne 0) \)cắt trục \( Ox,Oy\) hay đi qua một điểm nào đó.
Phương pháp:
Ta sử dụng kiến thức: Đồ thị hàm số \(y = ax + b\,(a \ne 0)\) đi qua điểm \(M\left( {{x_0};{y_0}} \right)\) khi và chỉ khi \({y_0} = a{x_0} + b.\)
Dạng 4: Tính đồng quy của ba đường thẳng
Phương pháp:
Để xét tính đồng quy của ba đường thẳng cho trước, ta thực hiện các bước sau
Bước 1. Tìm tọa độ giao điểm của hai đường thẳng trong ba đường thẳng đã cho.
Bước 2. Kiểm tra xem nếu giao điểm vừa tìm được thuộc đường thằng còn lại thì kết luận ba đường thẳng đó đồng quy.
III. Bài tập mẫu Đồ thị của hàm số y = ax + b
Cho hàm số \(y = \left( {a - 1} \right)x + a. \)
a) Xác định giá trị của \(a\) để đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 2.
b) Xác định giá trị của \(a\) để đồ thị hàm số cắt trục tung tại điểm có hoành độ bằng -3.
c) Vẽ đồ thị của hai hàm số ứng với giá trị của \(a\) tìm được ở các câu a) , b) trên cùng hệ trục tọa độ \(Oxy\) và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.
a) Hàm số \(y = \left( {a - 1} \right)x + a\,\,\,\,\left( {a \ne 1} \right)\) là hàm số bậc nhất có đồ thị hàm số cắt trục tung tại điểm có tung độ bằng \(y = 2\) nên \(a = 2\).
b) Hàm số \(y = \left( {a - 1} \right)x + a\,\,\,\,\left( {a \ne 1} \right)\) là hàm số bậc nhất có đồ thị hàm số cắt trục hoành tại điểm có hoành độ \(x = -3 \)nên tung độ giao điểm này bằng 0.
Ta có:
\(\eqalign{ & 0 = \left( {a - 1} \right)\left( { - 3} \right) + a \cr & \Leftrightarrow - 3a + 3 + a = 0 \cr & \Leftrightarrow - 2a = - 3 \Leftrightarrow a = 1,5 \cr} \)
c) Khi \(a = 2\) thì ta có hàm số: \(y = x + 2\)
Khi \(a = 1,5\) thì ta có hàm số: \(y = 0,5x + 1,5\)
* Vẽ đồ thị của hàm số \(y = x + 2\)
Cho \(x = 0\) thì \(y = 2.\) Ta có: \(A(0;2)\)
Cho \(y = 0\) thì \(x = -2\). Ta có: \(B(-2;0)\)
Đường thẳng AB là đồ thị hàm số \(y = x + 2\).
* Vẽ đồ thị của hàm số \(y = 0,5x + 1,5\)
Cho \(x = 0\) thì \( y = 1,5\). Ta có: \(C(0;1,5)\)
Cho \(y = 0\) thì \(x = -3\). Ta có : \(B(-3;0)\)
Đường thẳng CD là đồ thị hàm số \( y = 0,5x + 1,5\)
* Tọa độ giao điểm của hai đường thẳng .
Ta có:
\(M(x_1;y_1)\) thuộc đường thẳng \(y = x + 2\) nên \({y_1} = {x_1} + 2\)
\(M(x_1;y_1)\) thuộc đường thẳng \(y = 0,5x + 1,5\) nên \({y_1} = 0,5{x_1} + 1,5\)
Suy ra:
\(\eqalign{ & {x_1} + 2 = 0,5{x_1} + 1,5 \cr & \Leftrightarrow 0,5{x_1} = - 0,5 \cr & \Leftrightarrow {x_1} = - 1 \cr} \)
\({x_1} = - 1 \Rightarrow {y_1} = - 1 + 2 = 1 \)
Vậy tọa độ giao điểm của hai đường thẳng là \(M(-1;1)\).
=>> Xem thêm nhiều bài tập khác trong chuyên đề Đồ thị của hàm số y = ax + b lớp 9 để củng cố kiến thức và rèn luyện kỹ năng làm bài
-------------------------------
Hy vọng với hệ thống kiến thức lý thuyết Đồ thị của hàm số y = ax + b trên đây, các em sẽ có thêm một tài liệu học tập hữu ích để học tốt hơn môn Toán 9. Chúc các em luôn học tốt và đạt kết quả cao!