Đề thi tuyển sinh trường chuyên Trần Hưng Đạo (tỉnh Bình Thuận) môn Toán có lời giải chi tiết dành cho các em học sinh lớp 9 chuẩn bị thi vào 10 năm học 2020/2021 tham khảo và so sánh đối chiếu kết quả.
Chi tiết đề thi như sau:
Đề thi
Bài 1. (2,0 điểm)
a) Tính giá trị biểu thức \(A = \sqrt{5+2\sqrt 6} + \sqrt{5-2\sqrt 6}\)
b) Rút gọn biểu thức
\( B = \dfrac{x+ \sqrt x}{1-x} + \dfrac{4-5 \sqrt x}{1-\sqrt x} \)
Với \(x\geq 0; x ≠1\)
Bài 2. (2,0 điểm)
a) Vẽ đồ thị hàm số \(y = -\dfrac{1}2 x^2\).
b) Giải phương trình:
\((x-2)(x-1)(x+3)(x+4) - 24 = 0\)
Bài 3. (2,0 điểm)
Cho phương trình
\(2x^2 - 4mx -2m^2 -1 = 0\) (1)
(với m là tham số)
a) Chứng tỏ phương trình (1) luôn có hai nghiệm phân biệt với mọi m.
b) gọi x1, x2 là hai nghiệm của phương trình (1) khi m = 3, không giải phương trình hãy tính giá trị của biểu thức:
\(Q = (8x_1^2 - 50x_1 - 70)(8x_2^2 - 50x_2 - 70) + 2094\)
Bài 4. (3,0 điểm)
Cho đường tròn (O;R) đường kính AB. Trên tia tiếp tuyến Ax của (O;R) lấy điểm C khác A. Kẻ tiếp tuyến CD với (O;R) (D là tiếp điểm, D khác A).
a) Chứng minh rằng tứ giác OACD nội tiếp được một đường tròn.
b) Đường thẳng vuông góc với AB tại O cắt tia BD tại E. Chứng minh rằng BD.BE = 2R².
c) Gọi F là trung điểm của OE. Chứng minh rằng ba điểm B, F, C thẳng hàng.
Bài 5. (1,0 điểm)
Cho tam giác ABC có AB = c, AC = b, BC = a. Chứng minh rằng:
\(Sin \dfrac{A}2 \leq \dfrac{a}{b+c}\).
Đây là đề thi Toán chung vào lớp 10 của trường chuyên Trần Hưng Đạo vừa diễn ra vào chiều 4/7/2020 dành cho tất cả các thí sinh đăng kí dự tuyển. Các thầy cô của Đọc tài liệu đã tiết hành giải đề thi này chi tiết như sau:
Đáp án
Đáp án đề thi tuyển sinh vào 10 môn Toán chuyên Trần Hưng Đạo đang được cập nhật. Nếu không thấy nội dung, hãy load lại link bạn nhé!
Xem thêm: Đáp án đề thi Toán vào lớp 10 chuyên Trần Hưng Đạo năm 2019
Bài 1.
a) \(A = \sqrt{5+2\sqrt 6} + \sqrt{5-2\sqrt 6}\)
\(= \sqrt{3+2\sqrt {3.2}+2} + \sqrt{3-2\sqrt {3.2}+2}\)
\(= \sqrt{(\sqrt 3 + \sqrt 2)^2} + \sqrt{(\sqrt 3 - \sqrt 2)^2}\)
\(=\sqrt 3 + \sqrt 2 + \sqrt 3 - \sqrt 2 = 2\sqrt 3\)
b)
Với \(x\geq 0; x ≠1\), ta có:
\( B = \dfrac{x+ \sqrt x}{1-x} + \dfrac{4-5 \sqrt x}{1-\sqrt x} \)
\(= \dfrac{x+ \sqrt x + (4-5 \sqrt x)(1+\sqrt x)}{(1-\sqrt x)(1+\sqrt x)}\)
\(= \dfrac{x+ \sqrt x + 4-\sqrt x - 5x}{(1-\sqrt x)(1+\sqrt x)}\)
\(= \dfrac{4(1-x)}{1-x} = 4\)
Bài 2.
a)
Các em nhớ kẻ bảng giá trị tọa độ rồi vẽ nhé:
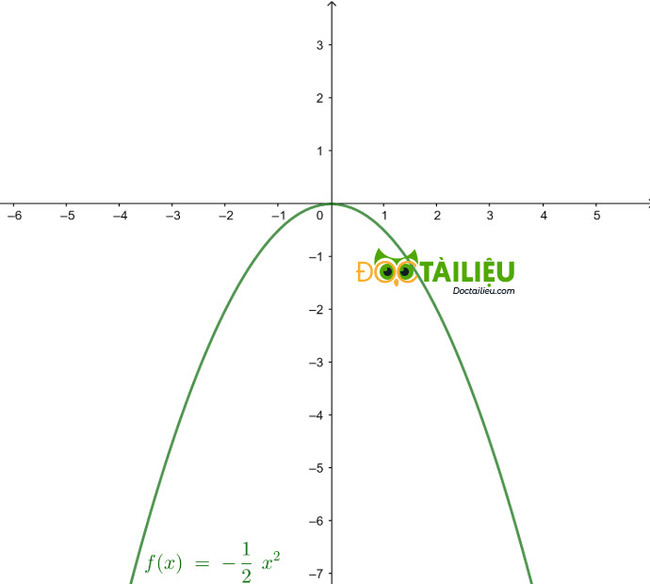
b)
\((x-2)(x-1)(x+3)(x+4) - 24 = 0\)
\(\Leftrightarrow (x^2-3x + 2)(x^2+7x + 12) - 24 = 0\)
\(\Leftrightarrow x^4 + 4x^3 -7x^2 -22x + 24- 24 = 0\)
\(\Leftrightarrow x^4 + 4x^3 -7x^2 -22x = 0\)
\(\Leftrightarrow x(x+2)(x^2+2x-11) = 0\)
\(\Leftrightarrow \left[ \matrix{ {x} = 0\hfill \cr {x} =-2 \hfill \cr x^2+2x-11 = 0\hfill \cr} \right. \)
\(\Leftrightarrow \left[ \matrix{ {x} = 0\hfill \cr {x} =-2 \hfill \cr x = -1 + 2\sqrt 3\hfill \cr x = -1 - 2\sqrt 3\hfill \cr} \right. \)
KL....
Bài 3.
Cho phương trình
\(2x^2 - 4mx -2m^2 -1 = 0\) (1)
(với m là tham số)
a)
Ta có:
\(\Delta' = 4m^2 - 2(-2m^2 -1) = 8m^2 +2 \geq 2 >0\)
với mọi m nên (1) luôn có hai nghiệm phân biệt (đpcm)
b)
Với m = 3, áp dụng hệ thức Vi-ét cho (1) ta có:
\(\left\{ \matrix{ x_1+x_2 = 2m = 6 \hfill \cr x_1x_2 = -m^2 -\dfrac{1}2 = -\dfrac{19}2 \hfill \cr} \right.\)
Ta có:
\(Q = (8x_1^2 - 50x_1 - 70)(8x_2^2 - 50x_2 - 70) + 2094\)
\(= 64x_1^2x_2^2 - 400(x_1^2x_2 + x_2^2x_1)+ 2500x_1x_2 - 560(x_1^2+x_2^2)+3500(x_1+x_2)+ 4900 + 2094\)
\(= 64x_1^2x_2^2 - 400x_1x_2(x_1 + x_2)+ 2500x_1x_2 - 560(x_1+x_2)^2+1120x_1x_2+3500(x_1+x_2)+ 6994\)
\(= 64\left(\dfrac{-19}2\right)^2 + 400.\dfrac{19}2.6 - 2500.\dfrac{19}2 - 560.6^2-1120.\dfrac{19}2+3500.6+ 6994\)
\(= 2020\)
Bài 4.
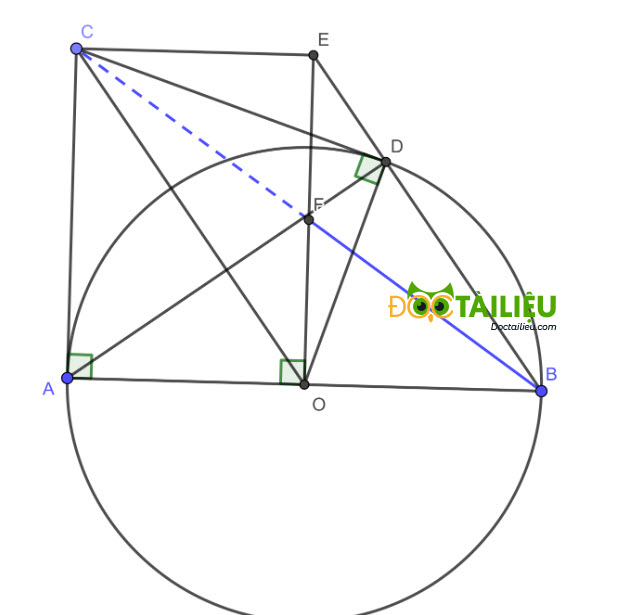
a)
Vì CA và CD là tiếp tuyến của (O) lần lượt tại A và D ⇒ ∠OAC = ∠ODC = 90° ⇒ A và D cùng thuộc đường tròn đường kính CO hay tứ giác OACD nội tiếp (đpcm).
b)
Xét △DBA và △OBE ta có:
∠EOB= ∠ADB = 90° (góc chắn đường kính)
Góc ∠ABD chung
Suy ra △DBA ∽△OBE ⇒ \(\dfrac{BD}{AB} = \dfrac{BO}{BE}\) ⇒ BD.BE = BO.AB = 2R.R = 2R² (đpcm)
c)
Vì △DBA ∽△OBE (cmt) ⇒ ∠BAD= ∠BEO = ∠DEO (1)
Theo tính chất tiếp tuyến, ta có ∠DCO = ∠ACO = 90° - ∠AOC = ∠DAO = ∠BAD (2)
Từ (1) và (2) suy ra ∠DEO = ∠DCO ⇒ 4 điểm D, E, O, C nội tiếp được ⇒ ∠CEO = ∠CDO = 90°.
Dễ thấy tứ giác AOEC có ∠CEO = ∠EOA= ∠OAC= 90° ⇒ AOEC là hình chữ nhật ⇒ CE // AB và EC = AO = OB.
Gọi F' là giao điểm của CB và EO, ta có:
CE // OB ⇒ \(\dfrac{EF'}{F'O} = \dfrac{EC}{OB} = 1\) ⇒ EF' = F'O hay F' là trung điểm EO, hay F' ≡ F
Hay B, F, C thẳng hàng (đpcm)
Bài 5.
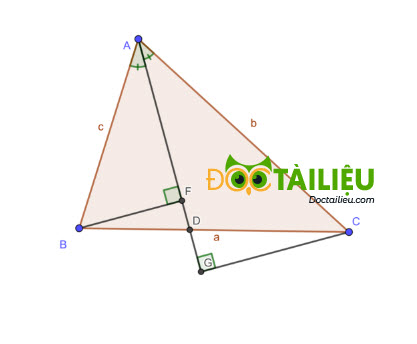
Vẽ phân giác trong AD của góc A như hình (D thuộc BC).
Từ B và C kẻ BF, CG ⊥ D (F, G thuộc AD).
Ta có: ∠BAD = ∠DAC = ∠BAC /2.
Áp dụng công thức sin, ta được:
\(sin \dfrac{A}2 = \dfrac{BF}c = \dfrac{GC}b\)
\(\Leftrightarrow \left\{ \matrix{ c.sin \dfrac{A}2 = BF \hfill \cr b.sin \dfrac{A}2 = GC \hfill \cr} \right. \)
\(\Leftrightarrow (b+c) sin \dfrac{A}2= BF + GC \)
Theo tính chất hình chiếu, ta có:
\((b+c) sin \dfrac{A}2= BF + GC \leq BD + DC = a \)
\(\Leftrightarrow Sin \dfrac{A}2 \leq \dfrac{a}{b+c}\)
(đpcm).Dấu bằng xảy ra
\(\Leftrightarrow \left\{ \matrix{ BF = BD \hfill \cr GC =DC \hfill \cr} \right. \) ⇔ BC ⊥ AD.
△ABC có AD vừa là phân giác vừa là đường cao ⇒ △ABC cân tại A.
-/-
Trên đây là toàn bộ nội dung của đáp án đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 - chuyên Trần Hưng Đạo do Đọc tài liệu thực hiện. Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành giúp các bạn hoàn thành tốt bài thi của mình.
Xem thêm: Đề thi vào 10 môn Văn năm 2020 chuyên Trần Hưng Đạo (Bình Thuận)
