Đề thi vào lớp 10 chuyên Toán trường chuyên Trần Hưng Đạo (tỉnh Bình Thuận) có hướng dẫn giải chi tiết dành cho các em học sinh lớp 9 chuẩn bị thi vào 10 năm học 2020/2021 tham khảo và so sánh đối chiếu kết quả.
Tham khảo thêm:
Đề thi vào 10 môn Toán năm 2020 chuyên Trần Hưng Đạo (Bình Thuận)Đề thi
Bài 1. (2,0 điểm)
Giải hệ phương trình:
\(\left\{ \matrix{ xy+x+y = 5 \hfill \cr xy+x^2+y^2 = 7 \hfill \cr} \right.\)
Bài 2. (2,0 điểm)
a) Cho p và p + 2 là các số nguyên tố lớn hơn 3. Chứng minh rằng p + 1 chia hết cho 6.
b) Tìm tất cả các số nguyên tố p sao cho 2p + 1 là lập phương của một số nguyên dương.
Bài 3. (2,0 điểm)
Cho các số thực \(x, y, z \geq 1\) thỏa mãn:
\(\dfrac{1}x+\dfrac{1}y+\dfrac{1}z = 2\)
Chứng minh rằng:
\(\sqrt{x+y+z} \geq \sqrt{x-1}+\sqrt{y-1}+\sqrt{z-1}\)
Bài 4. (3,0 điểm)
Cho tam giác ABC nhọn, các đường cao AD, BE, CF cắt nhau tại H. Cho K là một điểm tùy ý trên cạnh BC (K khác B, C). Kẻ đường kính KM của đường tròn ngoại tiếp tam giác BFK và đường kính KN của đường tròn ngoại tiếp tam giác CEK. Chứng minh rằng M, H, N thẳng hàng.
Bài 5. (1,0 điểm)
Cho 20 điểm phân biệt trong mặt phẳng. Chứng minh rằng tồn tại đường tròn chứa đúng 12 điểm đã cho bên trong và có đúng 8 điểm đã cho bên ngoài.
Đây là đề thi Toán chuyên vào lớp 10 của trường chuyên Trần Hưng Đạo vừa diễn ra vào chiều ngày 5/7/2020 dành cho tất cả các thí sinh đăng kí dự tuyển. Các thầy cô của Đọc tài liệu đã tiết hành giải đề thi này chi tiết như sau:
Đáp án đề thi tuyển sinh vào 10 môn Toán của chuyên Trần Hưng Đạo đang được cập nhật. Nếu không thấy nội dung, hãy load lại link bạn nhé!
Đáp án tham khảo
Gợi ý cách làm các câu hỏi trong đề thi vào 10 môn Toán hệ số 2 trường Chuyên Trần Hưng Đạo, Bình Thuận được Đọc tài liệu biên soạn và chia sẻ các em có thể tham khảo trong khi chờ đáp án chính thức nhé.
Bài 1.
\(\left\{ \matrix{ xy+x+y = 5 \hfill \cr xy+x^2+y^2 = 7 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ xy = 5 -(x+y) \hfill \cr (x+y)^2 - xy= 7 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ xy = 5 -(x+y) \hfill \cr (x+y)^2 - 5 + (x+y)= 7 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ xy = 5 -(x+y) \hfill \cr (x+y)^2 + (x+y)-12 = 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ xy = 5 -(x+y) \hfill \cr \left[ \matrix{ x+ y = 4 \hfill \cr x+y = 3 \hfill \cr} \right. \hfill \cr} \right.\)
\( \Leftrightarrow \left[ \matrix{ \left\{ \matrix{ x+ y = 4 \hfill \cr xy = 1 \hfill \cr} \right. \hfill \cr \left\{ \matrix{ x+ y = 3 \hfill \cr xy = 2 \hfill \cr} \right. \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ (x;y) = (2+\sqrt 3;2-\sqrt 3) \hfill \cr (x;y) = (2-\sqrt 3;2+\sqrt 3) \hfill \cr (x;y) = (1;2) \hfill \cr (x;y) = (2;1) \hfill \cr} \right.\)
Bài 2.
a)
Vì p và p + 2 là số nguyên tố lớn hơn 3 ⇒ p lẻ; p và p + 2 không chia hết cho 3.
Vì p lẻ ⇒ p + 1 chẵn hay p + 1 ⋮ 2 (1)
Vì p không chia hết cho 3 ⇒ p có dạng: p = 3k ± 1, (k ∈ ℕ*) mà p + 2 cũng không chia hết cho 3 ⇒ p = 3k - 1.
Suy ra p + 1 = 3k ⋮ 3 (2)
Từ (1) và (2), đồng thời (2;3) = 1 ⇒ p + 1 ⋮ 6 (đpcm).
b)
Theo bài ra ta có:
\(2p+1 = a^3\) (a ∈ ℕ*)
\(\Leftrightarrow 2p = a^3-1 = (a-1)(a^2+a+1)\) (*)
Dễ thấy \(a^2 + a + 1 > a-1\) (với mọi a ∈ ℕ*)
Lại có 2 và p là số nguyên tố nên \(p \geq 2\), suy ra:
(*) \(\Leftrightarrow \left[ \matrix{ \left\{ \matrix{ a-1 = 1 \hfill \cr a^2+a+1 = 2p \hfill \cr} \right. \hfill \cr \left\{ \matrix{ a-1 = 2 \hfill \cr a^2+a+1 = p \hfill \cr} \right. \hfill \cr} \right.\)
\(\Leftrightarrow \left[ \matrix{ \left\{ \matrix{ a= 2 \hfill \cr p = \dfrac{7}2 &(loại) \hfill \cr} \right. \hfill \cr \left\{ \matrix{ a= 3 \hfill \cr p = a^2+a+1 = 13 & (tm) \hfill \cr} \right. \hfill \cr} \right.\)
KL: p = 13 thỏa mãn....
Bài 3.
Áp dụng bất đẳng thức Bunhia-Cốpxki ta có:
\( \left(\sqrt{x.\dfrac{x-1}x}+\sqrt{y.\dfrac{y-1}y}+\sqrt{z.\dfrac{z-1}z}\right)^2 \leq (x+y+z) \left( \dfrac{x-1}x+\dfrac{y-1}y+\dfrac{z-1}z\right)\)
\(\Leftrightarrow \left(\sqrt{x-1}+\sqrt{y-1}+\sqrt{z-1}\right)^2 \leq (x+y+z) \left( 3 -\dfrac{1}x-\dfrac{1}y-\dfrac{1}z \right) = (x+y+z)(3-2) = x+y+z\)
\(\Leftrightarrow \sqrt{x-1}+\sqrt{y-1}+\sqrt{z-1} \leq \sqrt{x+y+z}\) (đpcm).
Dấu bằng xảy ra \(\Leftrightarrow x= y=z = \dfrac{3}2\).
Bài 4.
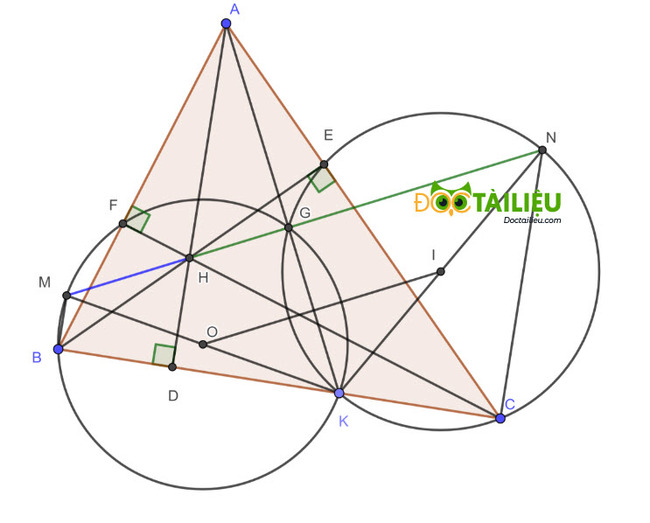
Gọi O, I lần lượt là tâm đường tròn ngoại tiếp △BFK và △CEK.
Xét △AFH và △ADB ta có:
Góc FAH chung
∠AFH = ∠ADB = 90° (gt)
Suy ra △AFH ∽ △ADB ⇒ \(\dfrac{AF}{AH}= \dfrac{AD}{AB}\) ⇒ AF.AB = AD.AH.
Tương tự △AEH ∽ △ADC ⇒ \(\dfrac{AE}{AH}= \dfrac{AD}{AC}\) ⇒ AE.AC = AD.AH = AF.AB (cmt) (1)
Gọi AK cắt (O) tại G.
Xét △AFG và △AKB ta có:
Góc FAG chung
∠AFG = 180° - ∠GFB = ∠GKB = ∠AKB
Suy ra △AFG ∽ △AKB ⇒ \(\dfrac{AF}{AG}= \dfrac{AK}{AB}\) ⇒ AF.AB = AK.AG (2)
Gọi AK cắt (I) tại G'.
Tương tự ta có △AEG' ∽ △AKC ⇒ \(\dfrac{AE}{AG'}= \dfrac{AK}{AC}\) ⇒ AK.AG' = AE.AC (3)
Từ (1) (2) và (3) suy ra AK.AG = AK.AG' ⇒ G ≡ G'.
Tức là G là giao điểm của (O),(I) và AK.
Lại có AK.AG = AD.AH ⇒ \(\dfrac{AK}{AD}= \dfrac{AH}{AG}\).
Xét △AHG và △AKD ta có:
Góc HAG chung
\(\dfrac{AK}{AD}= \dfrac{AH}{AG}\)
Suy ra △AHG ∽ △AKD ⇒ ∠AGH = ∠ADK = 90° ⇒ HG ⊥ KG (*)
Mặt khác ∠MGK = 90° (góc nội tiếp (O) chắn đường kính MK) ⇒ MG ⊥ KG (**)
Từ (*) và (**) suy ra MHG thẳng hàng.
Theo tính chất đường nối tâm, ta có: IO ⊥ GK.
Xét △KMN có OI là đường trung bình ⇒ IO // MN ⇒ MN ⊥ GK (***)
Từ (*) (**) và (***) suy ra M, H, G, N thẳng hàng, hay 3 điểm M, H, N thẳng hàng (đpcm).
Bài 5.
Gọi 20 điểm đã cho lần lượt là A1, A2, ..., A20.
Số đoạn thẳng tạo được từ 20 điểm này là: \(C_{20}^2 = 190\).
Với mỗi đoạn thẳng ta có 1 đường trung trực, tức là ta có tối đa 190 đường trung trực.
Vì số đường trung trực là hữu hạn, ta luôn tìm được 1 điểm I không thuộc bất kì 1 đường trung trực nào nêu trên, tức là khoảng cách từ I tới 20 điểm này đôi một khác nhau, hay:
IA1 ≠ IA2 ≠ IA3 ≠ ... ≠ IA20.
Không mất tính tổng quát, ta giả sử:
IA1 < IA2 < IA3 < .... < IA20.
Vì IA12 < IA13 nên ta luôn chọn được 1 số thực R sao cho IA12 < R < IA13.
Khi đó ta thấy đường tròn (I;R) là đường tròn chứa 12 điểm A1, A2..., A12 bên trong và 8 điểm A13, A14, ..., A20 nằm bên ngoài (đpcm).
Xem thêm: Đáp án đề thi Toán vào lớp 10 chuyên Trần Hưng Đạo năm 2019
-/-
Trên đây là toàn bộ nội dung của đáp án đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 - chuyên Trần Hưng Đạo do Đọc tài liệu thực hiện. Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành giúp các bạn hoàn thành tốt bài thi của mình.
