Đề thi và đáp án tuyển sinh vào lớp 10 môn Toán năm 2020 Bình Dương được ĐọcTàiLiệu cập nhật giúp các em học sinh tham khảo, so sánh kết quả với bài thi của mình.
Đề thi vào lớp 10 năm 2020

Chi tiết đề thi vào lớp môn Toán của tỉnh Bình Dương như sau:
|
Sở GD&ĐT Bình Dương ĐỀ CHÍNH THỨC |
KỲ THI TUYỂN SINH VÀO LỚP 10 NĂM HỌC: 2020 - 2021 Môn: Toán |
Bài 1 (2,0 điểm). Giải các phương trình, hệ phương trình sau:
1) \(x^2 + x - 12 = 0\)
2 ) \(x^4+ 8x^2 - 9 = 0\)
3) \(\left\{ \matrix{ 3x + y = -1 \hfill \cr 6x + y = 2 \hfill \cr} \right.\)
Bài 2 (1,5 điểm) Cho phương trình: \(x^2 – 2020x +2021 = 0\) có hai nghiệm phân biệt.
Không giải phương trình, tính giá trị của các biểu thức sau:
1) \(\dfrac{1}{x_1} + \dfrac{1}{x_2}\)
2) x\(_1^2 + x_2^2\)
Bài 3 (1,5 điểm) Cho Parabol (P): \(y = \dfrac{3}{2}x^2\) và đường thẳng (d): \(y = -\dfrac{3}{2}x + 3\)
1) Vẽ đồ thị của (P) và (d) trên cùng một mặt phẳng tọa độ.
2) Tìm tọa độ các giao điểm của (P) và (d) bằng phép tính.
Bài 4 (1,5 điểm) Cho biểu thức \(A = \left( \dfrac{1}{x-\sqrt{x}} + \dfrac{1}{\sqrt{x}-1}\right) : \dfrac{\sqrt{x}+1}{x\sqrt{x}-2x+\sqrt{x}}\)
với \(0 < x ≠ 1 \)
1) Rút gọn biểu thức A.
2) Tính giá trị của biểu thức A khi \(x = 8 – 2\sqrt{7} \)
Bài 5 (3,5 điểm) Cho đường tròn (O; 3cm) có đường kính AB và tiếp tuyến Ax. Trên Ax lấy điểm C sao cho AC = 8cm, BC cắt đường tròn (O) tại D. Đường phân giác của các CAD cắt đường tròn (O) tại M và cắt BC tại N.
1) Tính độ dài đoạn thẳng AD.
2) Gọi E là giao điểm của AD và MB. Chứng minh tứ giác MNDE nội tiếp được trong đường tròn.
3) Chứng minh tam giác ABN là tam giác cân.
4) Kẻ EF vuông góc AB (F thuộc AB). Chứng minh: N, E, F thẳng hàng.
--HẾT--
Đáp án đề tuyển sinh vào lớp 10 môn Toán Bình Dương 2020
Bài 1
1) \(x^2 + x - 12 = 0\)
\(\Leftrightarrow \left[ \matrix{ {x} = {3} \hfill \cr {x} = {-4} \hfill \cr} \right.\)
2) \(x^4 + 8x^2 - 9 = 0\)
\(\Leftrightarrow \left[ \matrix{ {x^2} = {1} \hfill \cr {x^2} = {-9} & (loại \space vì\space x^2 > 0) \hfill \cr} \right.\)
\(\Leftrightarrow x = ±1\)
3) \( \left\{ \matrix{ 3x + y = -1 \hfill \cr 6x + y = 2 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = 1 \hfill \cr y = -4 \hfill \cr} \right.\)
Bài 2
Ta có:
\(\Delta' = 1010^2 - 2021 > 0\) x1, x2 tồn tại.
Áp dụng hệ thức Vi-ét ta có:
\( \left\{ \matrix{ x_1+x_2 = 2020 \hfill \cr x_1x_2 = 2021 \hfill \cr} \right.\)
1) Thay vào ta có:
\(\dfrac{1}{x_1} + \dfrac{1}{x_2 } = \dfrac{x_1+x_2}{x_1x_2 } = \dfrac{2020}{2021} \)
2) Thay vào ta có:
\(x_1^2 + x_2^2 = (x_1+x_2)^2 - 2x_1x_2 = 2020^2 - 2.2021 = 4076358\)
Bài 3
1)
Các em nhớ kẻ bảng tọa độ điểm rồi vẽ nhé
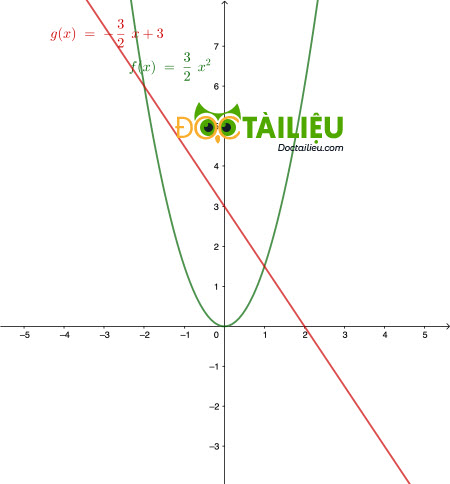
2. Hoành độ giao điểm của (P) và (d) là:
\(\dfrac{3}2 x^2 = -\dfrac{3}2x + 3\)
\(\Leftrightarrow x^2 + x -2 = 0\)
\(\Leftrightarrow \left[ \matrix{ {x} = 1 \Rightarrow y = \dfrac{3}2 \hfill \cr {x} = -2 \Rightarrow y = 6 \hfill \cr} \right.\)
KL.....
Bài 4.
1) Với \(0 < x ≠ 1 \) ta có:
\(A = \left( \dfrac{1}{x-\sqrt{x}} + \dfrac{1}{\sqrt{x}-1}\right) : \dfrac{\sqrt{x}+1}{x\sqrt{x}-2x+\sqrt{x}}\)
\(= \dfrac{1+\sqrt{x}}{\sqrt{x}(\sqrt{x}-1)} : \dfrac{\sqrt{x}+1}{\sqrt{x}(\sqrt{x}-1)^2}\)
\(= \dfrac{1+\sqrt{x}}{\sqrt{x}(\sqrt{x}-1)} . \dfrac{\sqrt{x}(\sqrt{x}-1)^2}{\sqrt{x}+1}\)
\(= \sqrt x -1\)
2) Với \(x = 8 - 2\sqrt 7 = 7 - 2\sqrt 7 + 1 = (\sqrt 7 -1)^2\)
Thay vào A ta có:
\(A = \sqrt x -1 = \sqrt{(\sqrt 7 -1)^2} - 1 = (\sqrt 7 -1) -1 = \sqrt 7 -2\)
Bài 5:
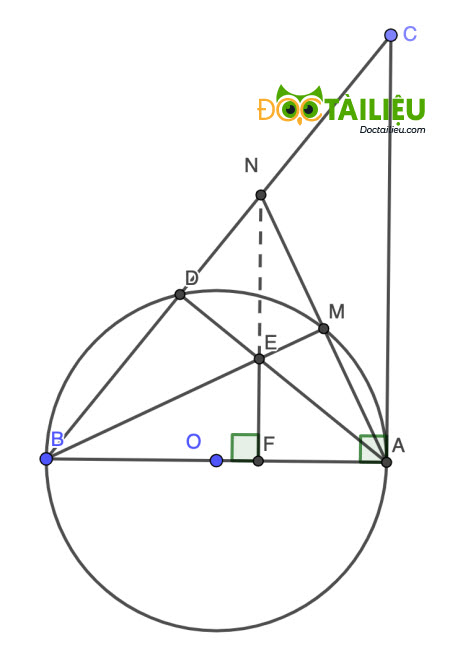
a) Ta thấy ∠ADB = 90° (góc nội tiếp chắn đường kính AB)
Ta có:
\(2 S_{\triangle ABC} = AB. AC = AD.BC\)
\(\Rightarrow AD = \dfrac{AB.AC}{BC} = \dfrac{AB.AC}{\sqrt{{AB}^2+{AC}^2}} = \dfrac{6.8}{6^2+8^2}= 4.8\) (cm)
2) Ta thấy:
∠ADB = ∠AMB = 90° (góc nội tiếp chắn đường kính AB)
Hay ∠NDE = ∠NME = 90° ⇒ D và M cùng thuộc đường tròn đường kính NE, hay tứ giác MNDE nội tiếp (đpcm).
3) Vì AN là phân giác của ∠DAC nên ∠DAN = ∠NAC = 90° - ∠NAB ⇒ ∠NAB = 90° - ∠DAN (1)
Xét △NAD vuông tại D ⇒ ∠DNA + ∠DAN = 90° hay ∠BNA = 90° - ∠DAN (2)
Từ (1) và (2) suy ra ∠NAB = ∠BNA.
Suy ra △NBA cân tại B (đpcm).
4)
Theo giả thiết ta có EF ⊥ AB (*)
Xét △NAB có BM ⊥ AN và AD ⊥ BN (cmt), BM cắt AD tại E ⇒ E là trực tâm của △NAB
Suy ra NE ⊥ AB (**)
Từ (*) và (**) suy ra E, F, N thẳng hàng (đpcm).
D
Hết
-/-
Đáp án đề thi tuyển sinh lớp 10 môn toán Bình Dương được thực hiện giải bởi tổ giải đề của Đọc Tài Liệu, khi sao chép nội dung này, yêu cầu ghi rõ nguồn từ https://doctailieu.com/.
Các môn thi khác
- Đề thi tuyển sinh vào lớp 10 môn Văn năm 2020 Bình Dương
- Đề thi tuyển sinh vào lớp 10 môn Anh năm 2020 Bình Dương
Trên đây là toàn bộ nội dung của đáp án đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 của tỉnh Bình Dương được Đọc Tài Liệu thực hiện sau khi kì thi chính thức diễn ra. Với nội dung này các em có thể so sánh đối chiếu kết quả bài thi của mình!
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành hữu ích với bạn trong kỳ thi này.
