Đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 vào trường Chuyên Trung học Thực hành TPHCM được Đọc Tài Liệu cập nhật giúp các em học sinh tham khảo.
Đề thi

Đáp án
Câu 1:
a) Xem hình
b)
Xét phương trình hoành độ giao điểm của (P) và (d') ta có:
\(-x^2 = -mx - 4\)
\(\Leftrightarrow x^2 -mx - 4 = 0\) (*)
Để (P) cắt (d') tại hai điểm phân biệt khi và chỉ khi (*) có hai nghiệm phân biệt, hay:
\(\Delta = m^2 + 16 >0 \) với mọi m.
Áp dụng hệ thức Vi-ét, ta có:
\(\left\{ \matrix{ x_1+x_2 = m \hfill \cr x_1x_2 = -4 \hfill \cr} \right.\)
Ta có:
\(y_1^2 + y_2^2 = 49\)
\(\Leftrightarrow x_1^4 + x_2^4 = 49\)
\(\Leftrightarrow (x_1^2 + x_2^2)^2 - 2x_1^2x_2^2 = 49\)
\(\Leftrightarrow [(x_1 + x_2)^2-2x_1x_2]^2 - 2x_1^2x_2^2 = 49\)
\(\Leftrightarrow (m^2+8)^2 - 2.(-4)^2= 49\)
\(\Leftrightarrow m^4 + 16m^2 -17 = 0\)
\(\Leftrightarrow \left[ \matrix{ m^2 = 1 \Rightarrow m = ±1 & (tm) \hfill \cr m^2 = -17 & (loại) \hfill \cr} \right.\)
KL...
Câu 2:
Để phương trình có 2 nghiệm phân biệt
⇔\(\Delta = 1^2 - 4 + 4m = 4m -3 >0 ⇔ m > \dfrac{3}4\)
Áp dụng hệ thức Vi-ét, ta có:
\(\left\{ \matrix{ x_1+x_2 = -1 \hfill \cr x_1x_2 = 1-m \hfill \cr} \right.\)
Ta có:
\(\dfrac{1}{x_1^2} + \dfrac{1}{x_2^2} \leq \dfrac{5}{(x_1x_2)^2}\) (đkxđ: \(x_1x_2 ≠ 0 ⇔ m ≠1\))
\(⇔ \dfrac{x_1^2 + x_2^2}{(x_1x_2)^2} \leq \dfrac{5}{(x_1x_2)^2}\)
\(⇔ x_1^2 + x_2^2 \leq 5\)
\(⇔ (x_1+ x_2)^2 - 2x_1x_2 \leq 5\)
\(⇔ 1 - 2(1-m) \leq 5\)
\(⇔ m \leq 3\)
Vậy \(\dfrac{3}4 < m \leq 3; m ≠ 1\)
Câu 3:
Ta có:
\(VT = \left( \sqrt a - \sqrt b \right) \left( \dfrac{a\sqrt a - b\sqrt b}{a-b} + \dfrac{1}{\dfrac{1}{\sqrt a}+\dfrac{1}{\sqrt b}} \right) \)
\(=\left( \sqrt a - \sqrt b \right) \left( \dfrac{(\sqrt a - \sqrt b)(a+ \sqrt {ab} + b)}{(\sqrt a - \sqrt b)(\sqrt a + \sqrt b)} + \dfrac{ \sqrt {ab} }{\sqrt a + \sqrt b} \right) \)
\(= \left( \sqrt a - \sqrt b \right) \left( \dfrac{a+ \sqrt {ab} + b}{\sqrt a + \sqrt b} + \dfrac{ \sqrt {ab} }{\sqrt a + \sqrt b} \right) \)
\(= \left( \sqrt a - \sqrt b \right) \left( \dfrac{a+ 2\sqrt {ab} + b}{\sqrt a + \sqrt b}\right) \)
\(= \left( \sqrt a - \sqrt b \right) \left( \dfrac{(\sqrt a + \sqrt b)^2}{\sqrt a + \sqrt b}\right) \)
\(= \left( \sqrt a - \sqrt b \right) \left( \sqrt a + \sqrt b\right) \)
\(= a-b\)
Hay \(\left( \sqrt a - \sqrt b \right) \left( \dfrac{a\sqrt a - b\sqrt b}{a-b} + \dfrac{1}{\dfrac{1}{\sqrt a}+\dfrac{1}{\sqrt b}} \right) = a-b\)
(đpcm)
KL....
Câu 4:
\(\dfrac{x^4}{1+x^2 - 2x} + \dfrac{1}{1-x} = 3+ x\)
ĐKXĐ: x ≠ 1.
\(⇔ \dfrac{x^4+1-x}{(x-1)^2} = 3+ x\)
\(⇔ x^4 - x + 1 = (3+ x)(x-1)^2\)
\(⇔ x^4 - x + 1 = (x + 3)(x^2 - 2x + 1)\)
\(⇔ x^4 - x + 1 = x^3 + x^2 - 5x + 3\)
\(⇔ x^4 -x^3 - x^2 + 4x - 2 = 0\)
\(⇔ (x^2 + x -1) (x^2 -2x + 2) = 0\)
Vì \(⇔x^2 -2x + 2 = (x-1)^2 + 1 > 0\) nên:
\(x^2 + x -1 = 0\)
\(⇔ \left[ \matrix{ {x} = \dfrac{-1+\sqrt 5}2 \hfill \cr {x} = \dfrac{-1-\sqrt 5}2 \hfill \cr} \right.\) (tm đkxđ)
KL....
Câu 5:
Gọi số bạn được 9 điểm là A (học sinh, A ∈ ℕ*)
Gọi số học sinh trong 1 tổ là X (học sinh, X ∈ ℕ*)
Vì lớp có 4 tổ, mỗi tổ có số học sinh bằng nhau ⇒ Tổng số học sinh của lớp là: 4X (4X > A)
Theo bài ra ta có:
\(9A + 8(4X - A) = 336\)
⇔ \(A + 32X = 336 > 32X ⇒ X < 10,5\)
Lại có \(4X > A ⇒ 336 = A + 32X < 4X + 32X = 36X ⇒ 9,3 < X\)
Mà \(X ∈ ℕ^*, 9,3 < X < 10,5 ⇒ X = 10\) (học sinh)
⇒ A = 336 - 32 x 10 = 16 (học sinh) (tm đk)
KL...
Câu 6:
Gọi cạnh tấm tôn ban đầu là a (cm; a > 4)
Ta có:
\(V_{hộp} = h.(a-4)^2 = 128 ⇔ (a-4)^2 = \dfrac{128}h = \dfrac{128}2 = 64\)
\(⇔ a- 4 = 8 ⇔ a= 12\) (cm)
Diện tích tấm tôn ban đầu là:
\(S = a^2 = 144 \space ({cm}^2)\)
KL....
Câu 7:
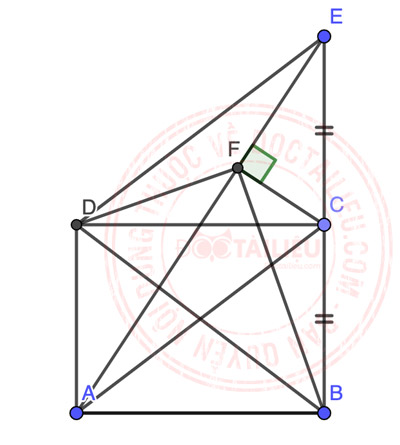
a)
Theo giả thiết, ta có: ∠ADC = ∠AFC = 90° ⇒ Tứ giác CADF nội tiếp đường tròn đường kính CA (đpcm)
⇒ ∠DFA = ∠DCA = ∠DBA
⇒ Tứ giác DFBA nội tiếp ⇒ ∠BFD + ∠BAD = 180° ⇒ ∠BFD = 180° - ∠BAD = 90° (đpcm)
b)
Xét △EFC và △EBA có:
Góc ∠FEC chung
∠EFC = ∠EBA = 90°
Suy ra △EFC ∽ △EBA ⇒ \(\dfrac{CF}{AB} = \dfrac{EC}{EA} \)
\(⇒ CF= \dfrac{EC.AB}{EA} = \dfrac{CB.AB}{\sqrt{{EB}^2 +{BA}^2}} =\dfrac{CB.AB}{\sqrt{{4CB}^2 +{BA}^2}} =\dfrac{3.4}{\sqrt{4.9 +16}} = \dfrac{6}{\sqrt{13}}\)
(cm)Ta có:
\(\dfrac{S_{\triangle DEF}}{S_{\triangle DAE}} = \dfrac{EF}{AE}\)
\(⇒ S_{\triangle DEF}= \dfrac{EF}{AE}.S_{\triangle DAE} = \dfrac{EF}{AE}(S_{ABED} - S_{\triangle EAB}) = \dfrac{EF}{AE}[\dfrac{1}2.(AD+BE).AB - \dfrac{1}2.BE.AB]\)
\(= \dfrac{\sqrt{{EC}^2-{FC}^2}}{\sqrt{{EB}^2+{BA}^2}}(\dfrac{1}2.3.AD.AB - \dfrac{1}2.2.AD.AB)\)
\(= \dfrac{\sqrt{{3}^2-{\dfrac{36}{13}}}}{\sqrt{4.3^2+4^2}}(\dfrac{1}2.3.3.4 - \dfrac{1}2.2.3.4)\)
\(= \dfrac{\dfrac{9}{\sqrt{13}}}{2\sqrt{13}}.6\)
\(= \dfrac{27}{13} \space ({cm}^2)\)
KL...
Câu 8:
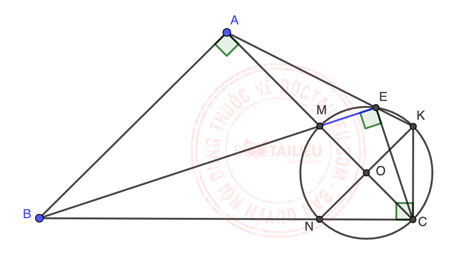
Vì △ABC vuông cân tại A ⇒ ∠ABC = ∠ACB = 45°.
△ONC cân tại O (do ON = OC) ⇒ ∠ONC = ∠OCN = 45° ⇒ ∠NOC = 90°.
Tương tự, ta có MNCK là hình vuông (do 2 đường chéo MC ⊥ NK và cắt nhau tại trung điểm mỗi đường)
Suy ra △ABC ∽ △KCM (hai △ cùng vuông cân) ⇒ \(\dfrac{AC}{BC} = \dfrac{KC}{MC} \) ⇒ \(\dfrac{AC}{KC} = \dfrac{BC}{MC} \)
Xét △CMB và △CKA, ta có:
\(\dfrac{AC}{KC} = \dfrac{BC}{MC} \) (cmt)
∠BCM = ∠ACK = 45°
Suy ra △CMB ∽ △CKA ⇒ ∠BMC = ∠AKC
Lại có tứ giác MEKC nội tiếp ⇒ ∠EKC + ∠EMC = 180° ⇒ ∠AKC = ∠EKC = 180° - ∠EMC
Suy ra ∠BMC = 180° - ∠EMC ⇒ ∠BMC + ∠EMC = 180° hay ∠BME = 180°
hay B,M,E thẳng hàng (đpcm).
Có thể các em quan tâm:
Trên đây là toàn bộ nội dung của đề thi tuyển sinh vào lớp 10 năm 2020 của chuyên Trung học Thực hành TPHCM được Đọc Tài Liệu thực hiện sau khi kì thi chính thức diễn ra.
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành hữu ích với bạn trong kỳ thi này.
