Bài 9 trang 46 sgk giải tích lớp 12 - cách làm và đáp án

Đề bài.

a) Khảo sát sự biến thiên và vẽ đồ thị (C)của hàm số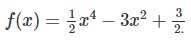 

b) Viết phương trình tiếp tuyến của đồ  thị(C) tại điểm có hoành độ là nghiệm của phương trình F'"(x) = 0

c) Biện luận theo tham số M số nghiệm của phương trình: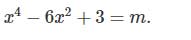 

Hướng dẫn giải.

a) Khảo sát và vẽ đồ thị hàm số qua các bước đã học.

b) Giải phương trình  F"(x) = 0 để tìm Xo. Sau đó viết phương trình tiếp tuyến của đồ thị hàm số (C) theo công thức:  Y = Y'(Xo)(X -Xo) + Y(Xo)

c) Đưa phương trình về dạng: 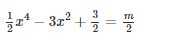 Sau đó dựa vào đồ thị ở câu a) để biện luận số nghiệm của phương trình. 

Đáp án bài 9 trang 46 sgk giải tích lớp 12

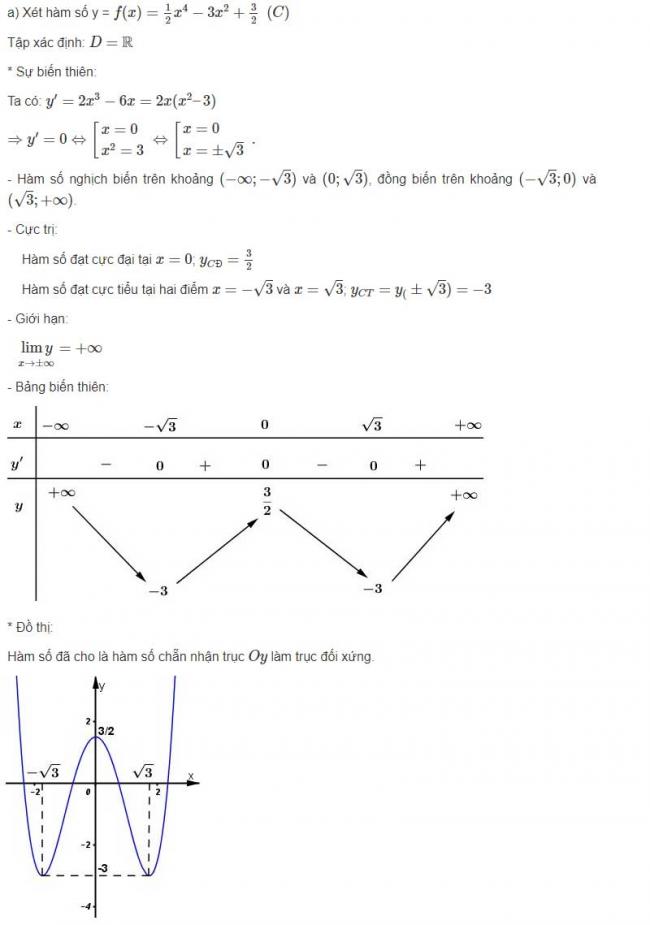
b) Ta có: f"(x) = 6x2 - 6 = 6(x2 - 1)

f"(x) = 0 ⇔ 6(x2 - 1) ⇔ x = ±1 => y = -1

Phương trình tiếp tuyến của (C) tại (-1; -1) là:

y = f'(-1)(x + 1) - 1 => y = 4x + 3

Phương trình tiếp tuyến của (C) tại (1; -1) là:

y = f'(1)(x - 1) - 1 => y = -4x + 3

c) Ta có: x4 - 6x2 + 3 = m

 

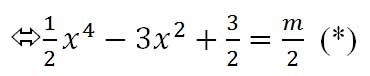
Số nghiệm của phương trình (*) chính bằng số giao điểm của đồ thị (C) và đường thẳng y = m/2.

Biện luận: Từ đồ thị:

+ m/2 < - 3 ⇔ m < -6: phương trình vô nghiệm.

+ m/2 = -3 ⇔ m = -6 : phương trình có 2 ngiệm.

+ -3 < m/2 < 3/2 ⇔ -6 < m < 3: phương trình có 4 nghiệm.

+ m/2 = 3/2 ⇔ m = 3: phương trình có 3 nghiệm.

+ m/2 > 3/2 ⇔ m > 3: phương trình có 2 nghiệm.

Vậy:

+) m < - 6 thì phương trình vô nghiệm.

+) m = - 6 hoặc m > 3 thì PT có 2 nghiệm.

+) m = 3 thì PT có 3 nghiệm.

+) – 6 < m < 3 thì PT có 4 nghiệm.