Giải bài 1 trang 63 sách giáo khoa hình học lớp 11

1. Đề bài

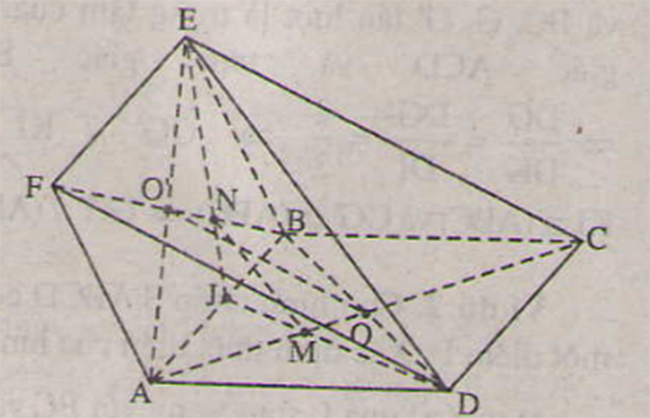
Cho hai hình bình hành ABCD và ABEF không cùng nằm trong một mặt phẳng.

• a) Gọi O và O’ lần lượt là tâm của các hình bình hành ABCD và ABEF. Chứng minh rằng đường thẳng OO’ song song và các mặt phẳng (ADF) và (BCF)
• b) Gọi M và N lần lượt là trọng tâm của tam giác ABD và ABE. Chứng minh đường thẳng MN song song với mặt phẳng (CEF).

2. Đáp án - hướng dẫn giải bài 1 trang 63

a) OO′ là đường trung bình của tam giác DBF nên OO′ // DF .

DF nằm trong mặt phẳng (ADF) nên OO′ // mp (ADF) .

Tương tự OO′ // CE mà CE nằm trong mặt phẳng (BCE ) nên OO′ // mp (BCE) .

b) Gọi J là trung điểm đoạn thẳng AB , Ta có:

JM/_JD = JN/_JE = 1/₃ ⇒ MN // ED

ED ⊂ (CEF) ⇒ M N / / ( C E F )