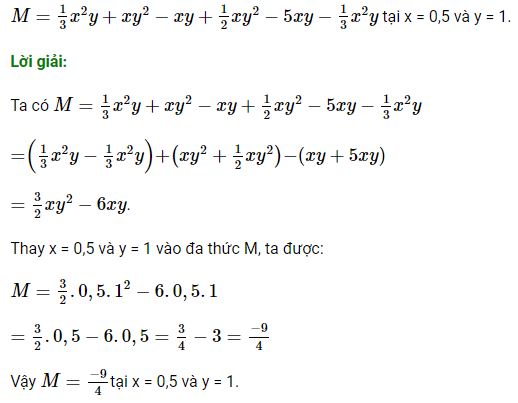Hướng dẫn trả lời câu hỏi và giải bài tập Toán 8 Kết nối tri thức tập 1 giúp học sinh nắm được các cách giải bài tập Chương 1: Đa thức chuẩn bị bài trước khi tới lớp và luyện tập giải toán tại nhà.
Chương 1 Bài 2: Đa thức
HĐ1 trang 11 Toán 8 Tập 1: Hãy nhớ lại, đa thức một biến là gì? Nêu một ví dụ về đa thức một biến.
Lời giải:
Đa thức một biến là tổng của những đơn thức của cùng một biến; mỗi đơn thức trong tổng đó gọi là một hạng tử của đa thức đó.
Một ví dụ về đa thức một biến: \(2x^3 – x^2 + 1\).
HĐ2 trang 11 Toán 8 Tập 1: Em hãy viết ra hai đơn thức tùy ý (không chứa biến, hoặc chứa từ một đến ba biến trong các biến x, y, z) rồi trao đổi với bạn ngồi cạnh để kiểm tra lại xem đã viết đúng chưa. Nếu chưa đúng, hãy cùng bạn sửa lại cho đúng.
Lời giải:
Học sinh viết ra hai đơn thức theo yêu cầu bài toán rồi trả đổi với bạn bên cạnh.
Sau đó cùng bạn sửa lại (nếu đơn thức đó viết chưa đúng).
HĐ3 trang 11 Toán 8 Tập 1: Viết tổng của bốn đơn thức mà em và bạn ngồi cạnh đã viết.
Lời giải:
Tùy theo các đơn thức mà em và bạn ngồi cạnh viết, ta có thể tìm được tổng khác nhau.
Chẳng hạn, bốn đơn thức được viết là: \(4x^2y; -\dfrac{1}{2}; x; 2x^2y\).
Tính tổng bốn đơn thức đó ta được:
\(4x^2y + (-\dfrac{1}{2})+x+2x^2y = (4x^2y + 2x^2y) + x - \dfrac{1}{2}\)
\(= 6x^2y+x-\dfrac{1}{2}\)
Luyện tập 1 trang 12 Toán 8 Tập 1: Biểu thức nào dưới đây là đa thức? Hãy chỉ rõ các hạng tử của mỗi đa thức ấy.
\(3xy^2 -1; x+\dfrac{1}{x}; \sqrt{2}x+\sqrt{3}y; x+\sqrt{xy}+y\)
Lời giải:
Các biểu thức là đa thức gồm: \(3xy^2-1; \sqrt{2}x+\sqrt{3}y\)
• Đa thức \(3xy^2 – 1\) có hai hạng tử \(3xy^2\) và – 1.
• Đa thức \(\sqrt{2}x+\sqrt{3}y\) có hai hạng tử \(\sqrt{2}x \)và \(\sqrt{3}y\)
Vận dụng trang 12 Toán 8 Tập 1: Mỗi quyển vở giá x đồng. Mỗi cái bút giá y đồng. Viết biểu thức biểu thị số tiền phải trả để mua:
a) 8 quyển vở và 7 cái bút;
b) 3 xấp vở và 2 hộp bút, biết rằng mỗi xấp vở có 10 quyển, mỗi hộp bút có 12 chiếc.
c) Mỗi biểu thức tìm được ở hai câu trên có phải là đa thức không?
Lời giải:
a) Giá tiền 8 quyển vở là: 8x (đồng);
Giá tiền 7 cái bút là: 7y (đồng)
Giá tiền 8 quyển vở và 7 cái bút là: 8x + 7y (đồng)
b) Mỗi xấp vở có 10 quyển nên 3 xấp vở có: 3 . 10 = 30 (quyển vở)
Giá tiền của 3 xấp vở là: 30x (đồng);
Mỗi hộp bút có 12 chiếc nên 2 hộp bút có: 12 . 2 = 24 (chiếc bút)
Giá tiền của 2 hộp bút là: 24y (đồng)
Giá tiền mua 3 xấp vở và 2 hộp bút là: 30x + 24y (đồng)
c) Hai đa thức tìm được ở hai câu trên lần lượt là: 8x + 7y; 30x + 24y đều là các đa thức.
Câu hỏi trang 12 Toán 8 Tập 1: Đa thức nêu trong tình huống mở đầu có phải là đa thức thu gọn không?
Lời giải:
Đa thức nêu trong tình huống mở đầu là \(x^2 + y^2 +\dfrac{1}{2}xy\) là đa thức thu gọn.
Luyện tập 2 trang 13 Toán 8 Tập 1: Cho đa thức
\(N = 5y^2z^2 - 2xy^2z + \dfrac{1}{3}x - 2y^2z^2 + \dfrac{2}{3}x^4 + xy^2z\)
a) Thu gọn đa thức N.
b) Xác định hệ số và bậc của từng hạng tử (tức là bậc của từng đơn thức) trong dạng thu gọn của N.
Lời giải:
a) Thu gọn đa thức N, ta được:
\(N = 5y^2z^2 - 2xy^2z + \dfrac{1}{3}x - 2y^2z^2 + \dfrac{2}{3}x^4 + xy^2z\)
\(= (5y^2z^2 - 2xy^2z) + (xy^2z - 2y^2z^2) + (\dfrac{1}{3}x + \dfrac{2}{3}x^4)\)
\(= 3y^2z^2 − xy^2z + x^4\)
.Vậy \(N = 3y^2z^2 − xy^2z + x^4\).
b) Dạng thu gọn của đa thức N có ba hạng tử gồm:
• Hạng tử \(3y^2z^2 \)có hệ số là 3 và bậc là 4;
• Hạng tử \(−xy^2z\) có hệ số là −1 và bậc là 4;
• Hạng tử \(x^4\) có hệ số là 1 và bậc là 4.
Luyện tập 3 trang 13 Toán 8 Tập 1: Với mỗi đa thức sau, thu gọn (nếu cần) và tìm bậc của nó:
a) \(Q = 5x^2 – 7xy + 2,5y^2 – 8,3y + 1\);
b) \(H = 4x^5 - \dfrac{1}{2}x^3y + \dfrac{3}{4}x^2y^2 - 4x^5 + 2y^2 - 7\)
Lời giải:
a) Đa thức Q đã ở dạng thu gọn.
Đa thức \(Q = 5x^2 – 7xy + 2,5y^2 – 8,3y + 1\) có bậc là 2.
b) Ta có \(H = 4x^5 - \dfrac{1}{2}x^3y + \dfrac{3}{4}x^2y^2 - 4x^5 + 2y^2 - 7\)
\(= (4x^5 - 4x^5)- \dfrac{1}{2}x^3y + \dfrac{3}{4}x^2y^2 + 2y^2 - 7\)
\(= - \dfrac{1}{2}x^3y + \dfrac{3}{4}x^2y^2 + 2y^2 - 7\)
Đa thức H có bậc là 4.
Tranh luận trang 14 Toán 8 Tập 1: Bạn Trang nêu vấn đề: Một đa thức bậc hai thu gọn với hai biến (x và y) mà mỗi hạng tử của nó đều có hệ số bằng 1 thì có nhiều nhất là mấy hạng tử? Có ba bạn trả lời như sau:
Anh: Có 3 hạng tử.
Bình: Có 5 hạng tử.
Chung: Có 6 hạng tử.
Em hãy nêu ý kiến của mình và cho biết đó là đa thức nào.
Lời giải:
Một đa thức bậc hai thu gọn với hai biến (x và y) mà mỗi hạng tử của nó đều có hệ số bằng 1 thì có nhiều nhất là 6 hạng tử, đó là đa thức\( x^2 + y^2 + xy + x + y + 1\).
Bài 1.8 trang 14 Toán 8 Tập 1: Trong các biểu thức sau, biểu thức nào là đa thức?
\(-x^2+3x+1; \dfrac{x}{\sqrt{5}}; x-\dfrac{\sqrt{5}}{x}; 2024; 3x^2y^2 - 5x^3y+2,4; \dfrac{1}{x^2+x+1}\)
Lời giải:
• Các biểu thức \(−x^2 + 3x + 1; 3x^2y^2 – 5x^3y + 2,4\) là các đa thức;
• Ta có \(\dfrac{x}{\sqrt{5}} = \dfrac{1}{\sqrt{5}}x\)
Các biểu thức \(\dfrac{1}{\sqrt{5}}x; 2024\) là các đơn thức nên \(\dfrac{x}{\sqrt{5}}; 2024\) cũng là các đa thức.
• Các biểu thức \(x-\dfrac{\sqrt{5}}{x}; \dfrac{1}{x^2+x+1}\) không phải là đa thức.
Do đó, các biểu thức là đa thức gồm: \(-x^2+3x+1; \dfrac{x}{\sqrt{5}}; 2024; 3x^2y^2 - 5x^3y+2,4\)
Bài 1.9 trang 14 Toán 8 Tập 1: Xác định hệ số và bậc của từng hạng tử trong đa thức sau:
a) \(x2y – 3xy + 5x2y2 + 0,5x – 4\);
b) \(x\sqrt{2} - 2xy^3+y^3+7x^3y\)
Lời giải:
a) Đa thức \(x^2y – 3xy + 5x^2y^2 + 0,5x – 4\) có:
- Hạng tử \(x^2y\) có hệ số là 1, bậc là 3;
- Hạng tử –3xy có hệ số là –3, bậc là 2;
- Hạng tử \(5x^2y^2\) có hệ số là 5, bậc là 4;
- Hạng tử 0,5x có hệ số là 0,5, bậc là 1;
- Hạng tử –4 có hệ số là –4, bậc là 0.
b) Đa thức \(x\sqrt{2} - 2xy^3+y^3+7x^3y\) có
- Hạng tử \(x\sqrt{2}\) có hệ số là \(\sqrt{2}\), bậc là 1;
- Hạng tử \(−2xy^3\) có hệ số là −2, bậc là 4;
- Hạng tử \(y^3\) có hệ số là 1, bậc là 3;
- Hạng tử \(−7x^3y\) có hệ số là −7, bậc là 4.
Bài 1.10 trang 14 Toán 8 Tập 1: Thu gọn đa thức:
a) \(5x^4 – 2x^3y + 20xy^3 + 6x^3y – 3x^2y^2 + xy^3 – y^4\);
b) \(0,6x^3 + x^2z – 2,7xy^2 + 0,4x^3 + 1,7xy^2\).
Lời giải:
a) \(5x^4 – 2x^3y + 20xy^3 + 6x^3y – 3x^2y^2 + xy^3 – y^4\)
\(= 5x^4 + (6x^3y – 2x^3y) + (20xy^3 + xy^3) – 3x^2y^2 – y4\)
\(= 5x^4 + 4x^3y + 21xy^3 – 3x^2y^2 – y^4.\)
b) \(0,6x^3 + x^2z – 2,7xy^2 + 0,4x^3 + 1,7xy^2\)
\(= (0,6x^3 + 0,4x^3) + x^2z + (1,7xy^2– 2,7xy^2)\)
\(= x^3 + x^2z – xy^2.\)
Bài 1.11 trang 14 Toán 8 Tập 1: Thu gọn (nếu cần) và tìm bậc của mỗi đa thức sau:
a) \(x^4 – 3x^2y^2 + 3xy^2 – x^4 + 1\);
b) \(5x^2y + 8xy – 2x^2 – 5x^2y + x^2.\)
Lời giải:
a) Đa thức \(x^4 – 3x^2y^2 + 3xy^2 – x^4 + 1\) có bậc là 4.
b) Ta có: \(5x^2y + 8xy – 2x^2 – 5x^2y + x^2\)
\(= (5x^2y – 5x^2y) + 8xy + (x^2– 2x^2) = 8xy – x^2.\)
Đa thức \(8xy – x^2\) có bậc là 2 nên đa thức \(5x^2y + 8xy – 2x^2 – 5x^2y + x^2\) có bậc là 2.
Bài 1.12 trang 14 Toán 8 Tập 1: Thu gọn rồi tính giá trị của đa thức:
Bài 1.13 trang 14 Toán 8 Tập 1: Cho đa thức \(P = 8x^2y^2z – 2xyz + 5y^2z – 5x^2y^2z + x^2y^2 – 3x^2y^2z.\)
a) Thu gọn và tìm bậc của đa thức P;
b) Tính giá trị của đa thức P tại x = –4; y = 2 và z = 1.
Lời giải:
a) Ta có: \(P = 8x^2y^2z – 2xyz + 5y^2z – 5x^2y^2z + x^2y^2 – 3x^2y^2z\)
\(= (8x^2y^2z – 3x^2y^2z– 5x^2y^2z) + x^2y^2– 2xyz + 5y^2z\)
\(= x^2y^2– 2xyz + 5y^2z.\)
b) Thay x = –4; y = 2 và z = 1 vào đa thức P, ta được:
\((–4)^2 . 2^2– 2 . (–4) . 2 . 1 + 5 . 2^2 . 1 = 16 . 4 + 8 . 2 + 5 . 4\)
= 64 + 16 + 20 = 100.
Vậy P = 100 tại x = –4; y = 2 và z = 1.
-//-
Hy vọng với nội dung trả lời chi tiết câu hỏi trong Bài 2: Đa thức giúp học sinh nắm được nội dung bài học và ghi nhớ những nội dung chính, quan trọng trong chương trình học Toán học 8.