Bài 41 trang 128 SGK Toán 9 tập 1

Những nội dung dưới đây không chỉ giúp bạn biết được cách làm, tham khảo đáp án bài 41 trang 128 SGK Toán 9 tập 1 mà còn hỗ trợ bạn ôn tập để nắm vững các kiến thức chương 1 phần hình học Đường tròn Toán 9 đã được học trên lớp.

Đề bài 41 trang 128 SGK Toán 9 tập 1

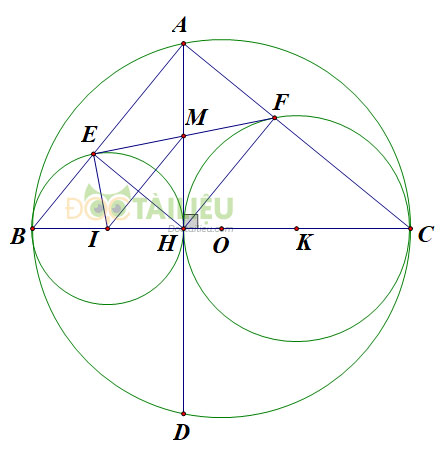
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.

Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF. 

a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O); (K) và(O); (I) và (K).

b) Tứ giác AEHF là hình gì? Vì sao?

c) Chứng minh đẳng thức \(AE.AB = AF.AC\)

d) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K)

e) Xác định vị trí của điểm H để EF có độ dài lớn nhất.

» Bài tập trước: Bài 40 trang 123 SGK Toán 9 tập 1

Giải bài 41 trang 128 SGK Toán 9 tập 1

Hướng dẫn cách làm

a) Vị trí tương đối của hai đường tròn (O;R) và (O';r) (\(R \ge r\) )

- TH1: 2 đường tròn cắt nhau (có 2 điểm chung) khi và chỉ khi : R - r < OO' < R + r

- TH2: 2 đường tròn tiếp xúc nhau (1 điểm chung)

+) Tiếp xúc trong khi và chỉ khi OO' = R - r >0

+) Tiếp xúc ngoài khi và chỉ khi OO' = R + r

b) Chứng minh tứ giác có ba góc vuông dựa vào kiến thức : “Tiếp tuyến của đường tròn vuông góc với bán kính tại tiếp điểm.

c) Dùng hệ thức lượng về chiều cao và độ dài hình chiếu của các cạnh góc vuông lên cạnh huyền : \({h^2} = b'.c'\) 

d) Chứng minh 1 đường thẳng là tiếp tuyến của 1 đường tròn thì ta chứng minh cho đường thẳng đó vuông góc với bán kính tại 1 điểm thuộc đường tròn.

e) Biểu diễn độ dài \(EF\) theo độ dài của \(AH\) rồi biện luận để tìm vị trí của dây đó vuông góc với \(BC\). 

Đáp án chi tiết

Dưới đây là các cách giải bài 41 trang 128 SGK Toán 9 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

a) \(OI = OB – IB\) nên (I) tiếp xúc trong với (O) 

\(OK = OC – KC\) nên (K) tiếp xúc trong với (O)

\(IK = IH + KH\) nên (I) tiếp xúc ngoài với (K)

b) \(\widehat {BEH} = 90°\) (E thuộc đường tròn đường kính BH)

\( \Rightarrow \widehat {A{\rm{E}}H} = {90^0}\)

Tương tự có \(\widehat {AFH} = {90^0};\widehat {BAC} = {90^0}\)

Tứ giác AEHF có \(\widehat {EAF} = \widehat {AEH} = \widehat {AFH} = {90^0}\) nên là hình chữ nhật.

c) ∆ABH vuông tại H, HE là đường cao nên \(AH^2 = AE. AB\)

∆ACH vuông tại H, HF là đường cao nên \(AH^2 = AF. AC\)

Do đó \(AE. AB = AF. AC\) (vì cùng bằng \(AH^2\) )

d) Gọi M là giao điểm của AH và EF, ta có: \(ME = MF = MH = MA\) (do tứ giác AEHF là hình chữ nhật)

Xét ∆MEI và ∆MHI có:

\(ME = MH, IE = IH (=R)\), MI (cạnh chung)

Do đó \(∆MEI = ∆MHI\) (c.c.c)

\(\Rightarrow \widehat {MEI} = \widehat {MHI}\)

mà \(\widehat {MHI} = {90^0}\) (do AD vuông góc với BC) nên \(\widehat {MEI} = {90^0}\) 

⇒ ME hay EF là tiếp tuyến của đường tròn (I)

Chứng minh tương tự có EF là tiếp tuyến của đường tròn (K)

e) Ta có \(EF = AH\) mà \(AH ≤ AO = R\)

Do đó  \(EF ≤ R\), không đổi. Dấu “=” xảy ra \(⇔ H ≡ O\)

Vậy khi dây AD vuông góc với BC tại O thì EF có độ dài lớn nhất.

» Bài tiếp theo: Bài 42 trang 128 SGK Toán 9 tập 1

Trên đây là nội dung hướng dẫn trả lời bài 41 trang 128 SGK Toán 9 tập 1 được Đọc Tài Liệu chia sẻ để giúp bạn hoàn thành tốt bài làm của mình. Mong rằng những tài liệu giải Toán 9 của chúng tôi sẽ luôn là người bạn đồng hành để giúp bạn học tốt hơn môn học này.