Bài 34 trang 119 SGK Toán 9 tập 1

Đáp án bài 34 trang 119 SGK Toán 9 tập 1 được biên soạn bởi Đọc Tài Liệu nhằm mục đích tham khảo phương pháp làm bài. Tài liệu cũng giúp các bạn ôn tập nội dung kiến thức trong Toán 9 chương 1 phần hình học về vị trí tương đối của hai đường tròn.

Đề bài 34 trang 119 SGK Toán 9 tập 1

Cho hai đường tròn \((O;\ 20cm)\) và \((O'; 15cm)\) cắt nhau tại \(A\) và \(B\). Tính đoạn nối tâm \(OO'\), biết rằng \(AB=24cm.\) (Xét hai trường hợp: \(O\) và \(O'\) nằm khác phía đối với \(AB;\ O\) và \(O'\) nằm cùng phía đối với \(AB\)).

» Bài tập trước: Bài 33 trang 119 SGK Toán 9 tập 1

Giải bài 34 trang 119 SGK Toán 9 tập 1

Hướng dẫn cách làm

+) Nếu \((O)\) và \((O')\) cắt nhau tại \(A,\ B\) thì \(OO'\) là trung trực của \(AB\).

+) Định lí Pytago: \(\Delta{ABC}\) vuông tại \(A\) thì \(BC^2=AB^2+AC^2\).

Đáp án chi tiết

Dưới đây là các cách giải bài 34 trang 119 SGK Toán 9 tập 1 để các bạn tham khảo và so sánh bài làm của mình:

* TH1:  \(O\) và \(O'\) nằm khác phía đối với \(AB\) (h.a)

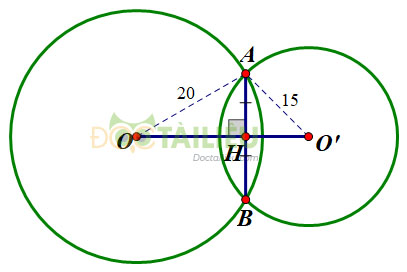
Vẽ dây cung \(AB\) cắt \(OO'\) tại \(H\). Theo định lí - trang 119, ta có:  \(AB\perp OO'\) và \(HA=HB=\dfrac{24}{2}=12cm\).

Xét tam giác \(AOH\) vuông tại \(H\), áp dụng định lí Pytago, ta có:

\(OA^2=OH^2+AH^2 \)

\(\Rightarrow OH^2=OA^2-AH^2\)

\(\Leftrightarrow OH^{2}=20^{2}-12^{2}=256\)

\(\Leftrightarrow OH=\sqrt{256}=16cm.\)

Xét tam giác \(AO'H\) vuông tại \(H\), áp dụng định lí Pytago, ta có:

\(AO'^2=AH^2+HO'^2\)

\(\Rightarrow HO'^2=AO'^2 - AH^2\)

\(\Leftrightarrow HO'^2=15^2-12^2=81\)

\(\Leftrightarrow HO'=\sqrt {81}=9(cm)\).

Khi đó  \(OO'=OH+HO'=16+9=25(cm).\)

*TH2: \(O\) và \(O'\) nằm cùng phía đối với \(AB\) (h.b)

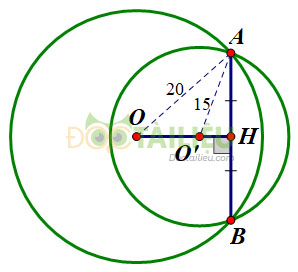
Tương tự TH1 ta có \(OH=16cm;O'H=9cm\)

Khi đó \(OO'=OH-O'H=16-9=7(cm).\)

» Bài tiếp theo: Bài 35 trang 122 SGK Toán 9 tập 1

Nội dung trên đã giúp bạn nắm được cách làm bài 34 trang 119 SGK Toán 9 tập 1. Hy vọng những bài hướng dẫn giải Toán 9 của Đọc Tài Liệu sẽ giúp các bạn hoàn thành bài tập chính xác và học tốt môn học này.