Bài 12 trang 72 SGK Toán 9 tập 2

Lời giải bài 12 trang 72 SGK Toán 9 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 9 chương 3 phần hình học để tự tin hoàn thành tốt các bài tập liên hệ giữa cung và dây.

Đề bài 12 trang 72 SGK Toán 9 tập 2

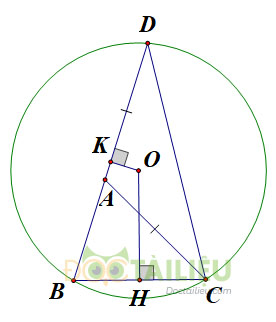
Cho tam giác \(ABC\). Trên tia đối của tia \(AB\) lấy một điểm \(D\) sao cho \(AD = AC\). Vẽ đường tròn tâm \(O\) ngoại tiếp tam giác \(DBC\). Từ \(O\) lần lượt hạ các đường vuông góc \(OH\), \(OK\) với \(BC\) và \(BD\) \((H \in BC, K \in BD)\).

a) Chứng minh rằng \(OH > OK\).

b) So sánh hai cung nhỏ \(\overparen{BD}\) và \(\overparen{BC}\).

» Bài tập trước: Bài 11 trang 72 SGK Toán 9 tập 2

Giải bài 12 trang 72 SGK Toán 9 tập 2

Hướng dẫn cách làm

a) Sử dụng định lý: "Tổng hai cạnh trong một tam giác luôn lớn hơn cạnh còn lại"

So sánh khoảng cách từ tâm đến dây cung:

Trong một đường tròn:

- Dây cung nào lớn hơn thì gần tâm hơn

- Dây cung nào gần tâm hơn thì lớn hơn.

b) Sử dụng: Định lý liên hệ giữa cung và dây: "Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

- Cung lớn hơn căng dây lớn hơn.

- Dây lớn hơn căng cung lớn hơn.

Đáp án chi tiết

Dưới đây là các cách giải bài 12 trang 72 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

a) Trong \(∆ABC\), có \(BC < BA + AC\) (tổng hai cạnh của một tam giác luôn lớn hơn cạnh còn lại).

Mà \(AC = AD\) suy ra \(BC < BA+AD\) hay \(BC<>.

Theo định lí về dây cung và khoảng cách từ dây đến tâm, ta có \(OH > OK\).

b) Ta có \(BC < BD\) (cmt)

nên suy ra \(\overparen{BC}\) nhỏ hơn \(\overparen{BD}\) ( liên hệ cung và dây) 

» Bài tiếp theo: Bài 13 trang 72 SGK Toán 9 tập 2

Trên đây là nội dung hướng dẫn trả lời bài 12 trang 72 SGK Toán 9 tập 2 được Đọc Tài Liệu chia sẻ để giúp bạn hoàn thành tốt bài làm của mình. Mong rằng những tài liệu giải Toán 9 của chúng tôi sẽ luôn là người bạn đồng hành để giúp bạn học tốt hơn môn học này.