Bài 11 trang 72 SGK Toán 9 tập 2

Bạn muốn giải bài 11 trang 72 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết, không chỉ tham khảo cách làm hoặc đáp án mà bài viết này còn giúp bạn nắm vững lại các kiến thức Toán 9 chương 3 phần hình học để tự tin giải tốt các bài tập khác về liên hệ giữa cung và dây.

Đề bài 11 trang 72 SGK Toán 9 tập 2

Cho hai đường tròn bằng nhau \((O)\) và \((O')\) cắt nhau tại hai điểm \(A\) và \(B\). Kẻ các đường kính \(AOC, AO'D\). Gọi \(E\) là giao điểm thứ hai của \(AC\) với đường tròn \((O')\).

a) So sánh các cung nhỏ \(\overparen{BC}, \overparen{BD}\).

b) Chứng minh rằng \(B\) là điểm chính giữa của cung \(\overparen{EBD}\) ( tức điểm \(B\) chia cung \(\overparen{EBD}\) thành hai cung bằng nhau: \(\overparen{BE}\) =  \(\overparen{BD}\) ).

» Bài tập trước: Bài 10 trang 71 SGK Toán 9 tập 2

Giải bài 11 trang 72 SGK Toán 9 tập 2

Hướng dẫn cách làm

* Chứng minh hai tam giác bằng nhau hoặc tam giác cân để suy ra hai dây bằng nhau.

Từ đó sử dụng định lý: Với hai cung nhỏ trong một đường tròn hay trong hai đường tròn bằng nhau:

+)  Hai cung bằng nhau căng hai dây bằng nhau.

+) Hai dây bằng nhau căng hai cung bằng nhau.

Đáp án chi tiết

Dưới đây là các cách giải bài 11 trang 72 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

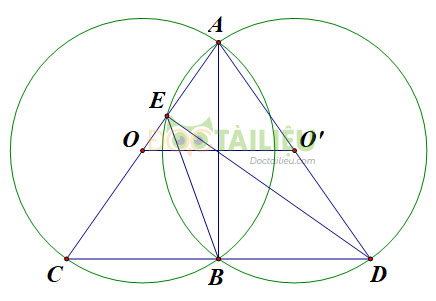
a) Vì \(\left( O \right)\) và \(\left( {O'} \right)\) cắt nhau tại hai điểm \(A\) và \(B\) nên \(OO' \bot AB\) (định lý)

Xét tam giác \(ADC\) có \(OO'\) là đường trung bình (vì \(O\) là trung điểm \(AC,O'\) là trung điểm \(AD\)) nên \(OO'//CD\) , suy ra \(AB \bot CD\) (quan hệ từ vuông góc đến song song).

Xét tam giác \(ADC\) có \(AC = AD\) (vì hai đường tròn \(\left( O \right)\) và \(\left( {O'} \right)\) có cùng bán kính) nên \(\Delta ACD\) cân tại \(A\) có \(AB\) là đường cao nên \(AB\) cũng là đường trung tuyến, suy ra \(BC = BD\) hay cung BC = cung BD  (vì \(\left( O \right)\) và \(\left( {O'} \right)\) là hai đường tròn bằng nhau).

b) Xét đường tròn \(\left( {O'} \right)\) có \(A,E,D\) cùng thuộc đường tròn và \(AD\) là đường kính nên tam giác \(AED\) vuông tại \(E \Rightarrow DE \bot AC \Rightarrow \widehat {DEC} = 90^\circ .\)

Xét tam giác \(DEC\) vuông tại \(E\) có \(B\) là trung điểm \(DC\left( {cmt} \right) \Rightarrow EB = \dfrac{{DC}}{2} = BD = EB\)

Suy ra  cung EB=cung BD (định lý), do đó \(B\) là điểm chính giữa cung \(ED.\).

» Bài tiếp theo: Bài 12 trang 72 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 11 trang 72 Toán hình học 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.