Đề thi vào 10 môn Toán tỉnh Quảng Bình năm 2024-2025 chính thức được Đọc tài liệu cập nhật nhanh và chính xác kèm đáp án bên dưới.
Đề thi vào lớp 10 môn Toán Quảng Bình 2023
Đáp án đang được cập nhật...

ĐÁP ÁN THAM KHẢO



Xem thêm thông tin tuyển sinh:
- Điểm chuẩn lớp 10 năm 2024 Quảng Bình
- Điểm thi tuyển sinh lớp 10 năm 2024 Quảng Bình
- Đề thi tuyển sinh lớp 10 môn Văn 2024 Quảng Bình
Tham khảo chi tiết đề thi chính thức các năm trước tại đây:
Đề thi vào lớp 10 môn Toán Quảng Bình 2023
Đề thi chính thức vào lớp 10 môn Toán năm 2023 tỉnh Quảng Bình được cập nhật ngay khi kết thúc thời gian làm bài thi môn toán ngày 07/06/2023.

ĐÁP ÁN THAM KHẢO
Câu 1.
1.
\(A= \dfrac{1}{\sqrt{a}+3} + \dfrac{6}{a-9}\) với a ≥ 0 và a ≠ 9
\(⇔A = \dfrac{1}{\sqrt{a}-3} + \dfrac{6}{(\sqrt{a}-3)(\sqrt{a}+3)} \)
\(= \dfrac{\sqrt{a}-3}{(\sqrt{a}-3)(\sqrt{a}+3)} + \dfrac{6}{(\sqrt{a}-3)(\sqrt{a}+3)} \)
\(= \dfrac{\sqrt{a}-3 + 6}{(\sqrt{a}-3)(\sqrt{a}+3)}\)
\(= \dfrac{\sqrt{a}+ 3}{(\sqrt{a}-3)(\sqrt{a}+3)}\)
\(= \dfrac{1}{\sqrt{a}-3}\)
Vậy \(A= \dfrac{1}{\sqrt{a}-3}\)
2. Để A = \(\dfrac{1}{2}\)
hay \(\dfrac{1}{\sqrt{a}-3} = \dfrac{1}{2} ⇔\sqrt{a}-3 = 2⇔\sqrt{a} = 5⇔a=25 (t/m)\)
Vậy với a = 25 thì A = \(\dfrac{1}{2}\)
Câu 2.

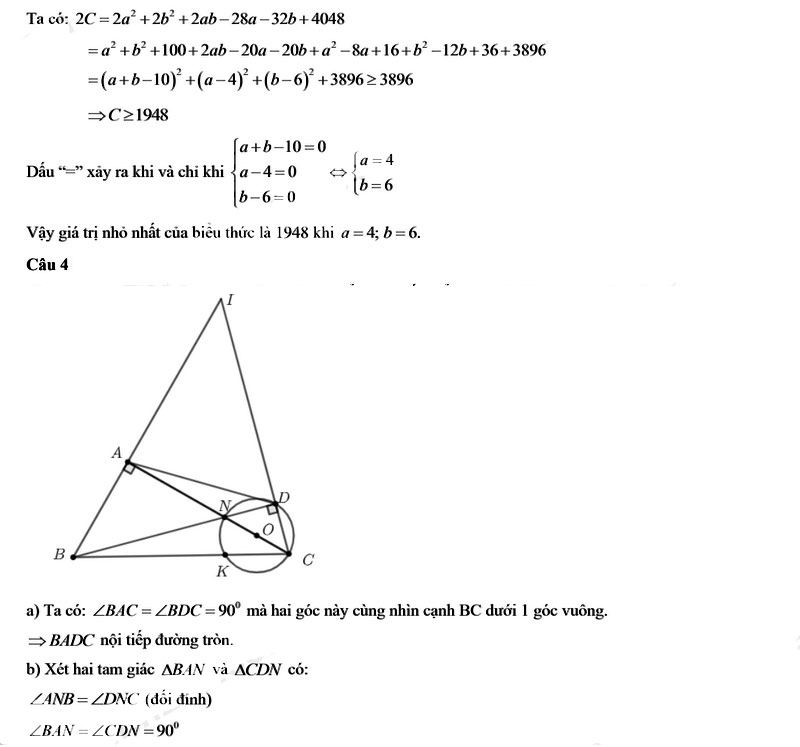
Câu 3.
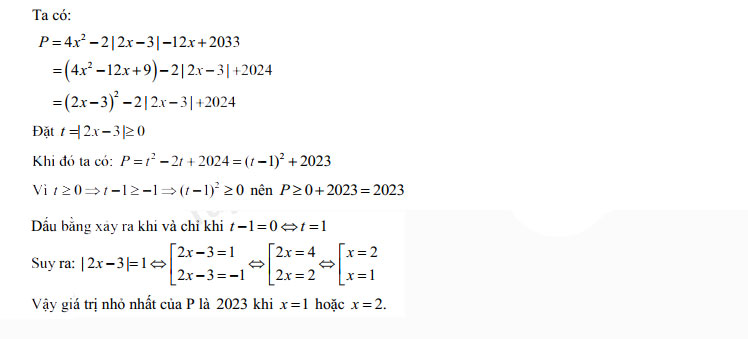
Câu IV
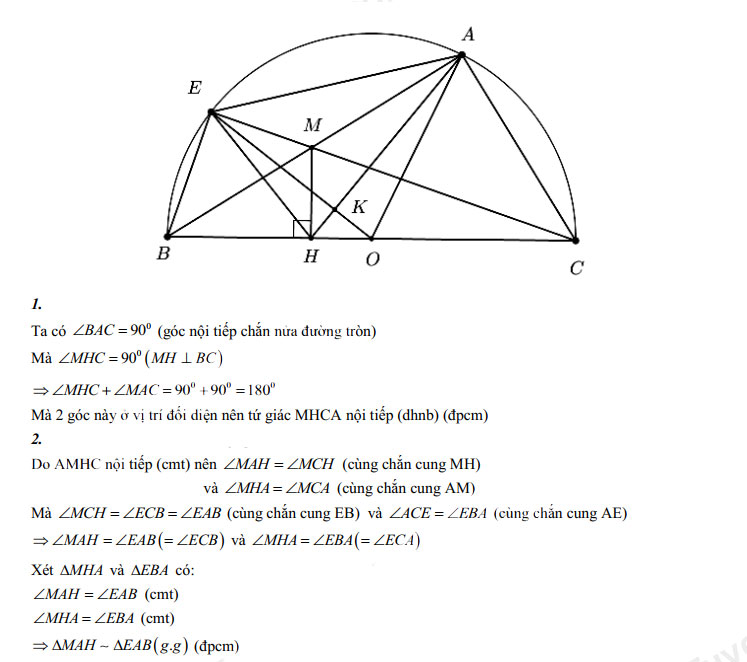
Cho nửa đường tròn tâm O đường kính BC và điểm A thuộc nửa đường tròn đó, (A khác B và C). Lấy điểm E thuộc cung AB (E khác A và B) sao cho BE ‹ AC, gọi M là giao điểm của AB và CE. Kẻ MH vuông góc với BC tại H.
1. Chứng minh tứ giác ACHM nội tiếp.
2. Chứng minh △BAE đồng dạng với △HAM
3. Gọi K là giao điểm của OE và HA. Chứng minh KE.KO = KA.KH.
BL:

Đề thi vào lớp 10 môn Toán Quảng Bình 2022

ĐÁP ÁN
Câu 1
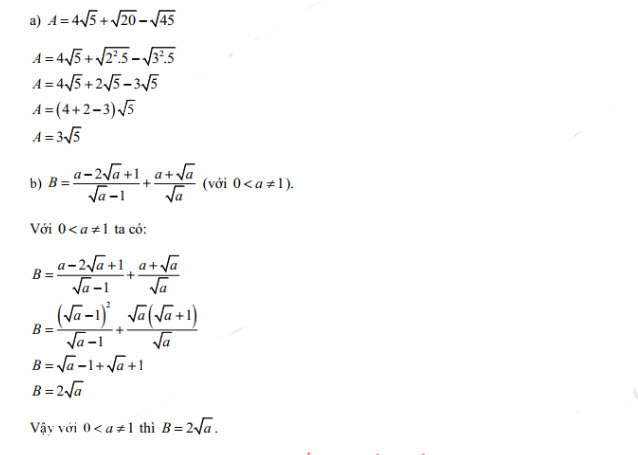
Câu 2
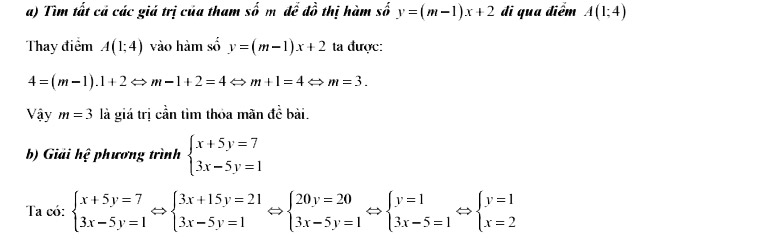
Câu 3

Câu 4
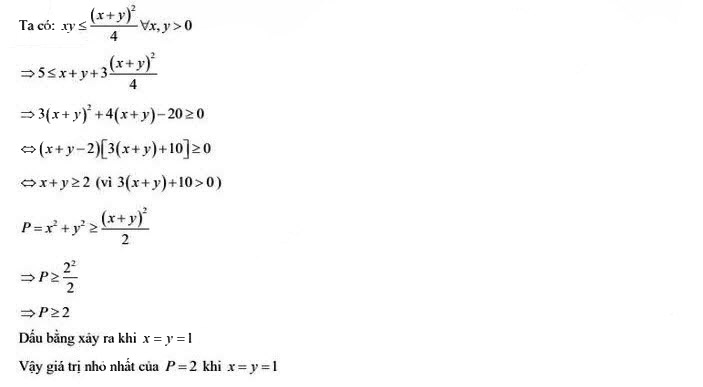
Câu 5

Đề thi tuyển sinh lớp 10 môn Toán Quảng Bình 2021
Đề thi chính thức vào lớp 10 môn Toán năm 2021 tỉnh Quảng Bình được cập nhật ngay khi kỳ thi diễn ra ngày 08/06/2021.


(Mã đề 002 có cách làm tương tự, các em tham khảo giải đề thi mã 001 dưới đây)
Đáp án mã 01
Câu 1
a) \(\begin{aligned} & A=\sqrt{8}-\sqrt{32}+\sqrt{50}\\ &A=\sqrt{8}-\sqrt{32}+\sqrt{50}\\ &A=\sqrt{2^{2} \cdot 2}-\sqrt{4^{2} \cdot 2}+\sqrt{5^{2} \cdot 2}\\ &A=2 \sqrt{2}-4 \sqrt{2}+5 \sqrt{2}\\ &A=(2-4+5) \sqrt{2}\\ &A=3 \sqrt{2}\\ &\text { Vậy } A=5 \sqrt{2} \text { . } \end{aligned}\)
b)
\(B=\left(3+\frac{a+\sqrt{a}}{\sqrt{a}+1}\right) \cdot\left(3-\frac{a-\sqrt{a}}{\sqrt{a}-1}\right)( với\,\,a \geq 0, a \neq 1).\)
Với \(a \geq 0, a \neq 1\) ta có:
\(B=\left(3+\frac{a+\sqrt{a}}{\sqrt{a}+1}\right) \cdot\left(3-\frac{a-\sqrt{a}}{\sqrt{a}-1}\right)\)
\(B=\left(3+\frac{\sqrt{a}(\sqrt{a}+1)}{\sqrt{a}+1}\right) \cdot\left(3-\frac{\sqrt{a}(\sqrt{a}-1)}{\sqrt{a}-1}\right)\)
\(B=(3+\sqrt{a}) \cdot(3-\sqrt{a})\)
B = 9 - a
Vậy với \(a \geq 0, a \neq 1\) thì B = 9-a.
Câu 2
a)
Để hàm số y=(m-1) x+2 đồng biến trên ℝ thì m-1>0 ⇒ m>1.
Vậy hàm số y=(m-1) x+2 đồng biển trên ℝ khi m>1.
b) \(\left\{\begin{array} { l } { 3 x + 2 y = 8 } \\ { 3 x - 4 y = 2 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { 6 y = 6 } \\ { 3 x + 2 y = 8 } \end{array} \Leftrightarrow \left\{\begin{array} { l } { y = 1 } \\ { 3 x + 2 = 8 } \end{array} \Leftrightarrow \left\{\begin{array}{l} y=1 \\ x=2 \end{array}\right.\right.\right.\right.\)
Câu 3.
a) \(\text { Với } m=1 \text { thì (1) trờ thành } x^{2}-6 x+5=0 \text { . }\)
Ta có a+b+c = 1-6+5=0 nên phương trình có 2 nghiệm phân biệt
\( \left[\begin{array}{l} x=1 \\ x=\frac{c}{a}=5. \end{array}\right.\)
Vậy khi m=1 thì tập nghiềm của phương trình là S= {1 ; 5}.
b) Phương trình (1) có hai nghiệm phân biệt
\(x_{1}, x_{2} \Leftrightarrow \Delta^{\prime}>0 \Leftrightarrow 9-m-4>0 \Leftrightarrow 5-m>0 \Leftrightarrow m<5\) .
Khi đó áp dụng hệ thức Vi- ét ta có
\(\left\{\begin{array}{l} x_{1}+x_{2}=6 \\ x_{1} x_{2}=m+4 \end{array}\right.\)
Khi đó ta có:
\(\begin{aligned} 2020\left(x_{1}+x_{2}\right)-2021 x_{1} x_{2}=2014 \\ \Leftrightarrow 2020.6-2021 .(m+4)=2014 \\ \Leftrightarrow 12120-2021 m-8084=2014 \\ \Leftrightarrow 2021 m=2022 \\ \Leftrightarrow m=\frac{2022}{2021}(\mathrm{tm}) \\ \text { Vậy } m=\frac{2022}{2021} . \end{aligned}\)
Câu 4.
Áp dụng BĐT Cô-si ta có
\(\begin{aligned} &\sqrt{16 a(15 a+b)} \leqslant \frac{16 a+15 a+b}{2}=\frac{31 a+b}{2}\\ &\sqrt{16 b(15 b+a)} \leq \frac{16 b+15 b+a}{2}=\frac{31 b+a}{2}\\ &\Rightarrow \sqrt{16 a(15 a+b)}+\sqrt{16 b(15 b+a)} \leq \frac{31 a+b+31 b+a}{2}=16(a+b)\\ &\Rightarrow \sqrt{a(15 a+b)}+\sqrt{b(15 b+a)} \leq 4(a+b)\\ &\Rightarrow \frac{a+b}{\sqrt{a(15 a+b)}+\sqrt{b(15 b+a)}} \geq \frac{1}{4}(d p c m)\\\end{aligned}\)
Dấu "=" xày ra khi và chi khi
\(\left\{\begin{array}{l} 16 a=15 a+b \\ 16 b=15 b+a \end{array} \Leftrightarrow a=b\right. \text { . } \)
Câu 5

Cùng ôn tập với đề thi vào 10 các năm trước đã được tổng hợp dưới đây:
Đề thi vào 10 môn Toán Quảng Bình các năm
Đề thi tuyển sinh lớp 10 môn Toán Quảng Bình năm 2020

Đáp án đề thi tuyển sinh lớp 10 môn toán Quảng Bình 2020


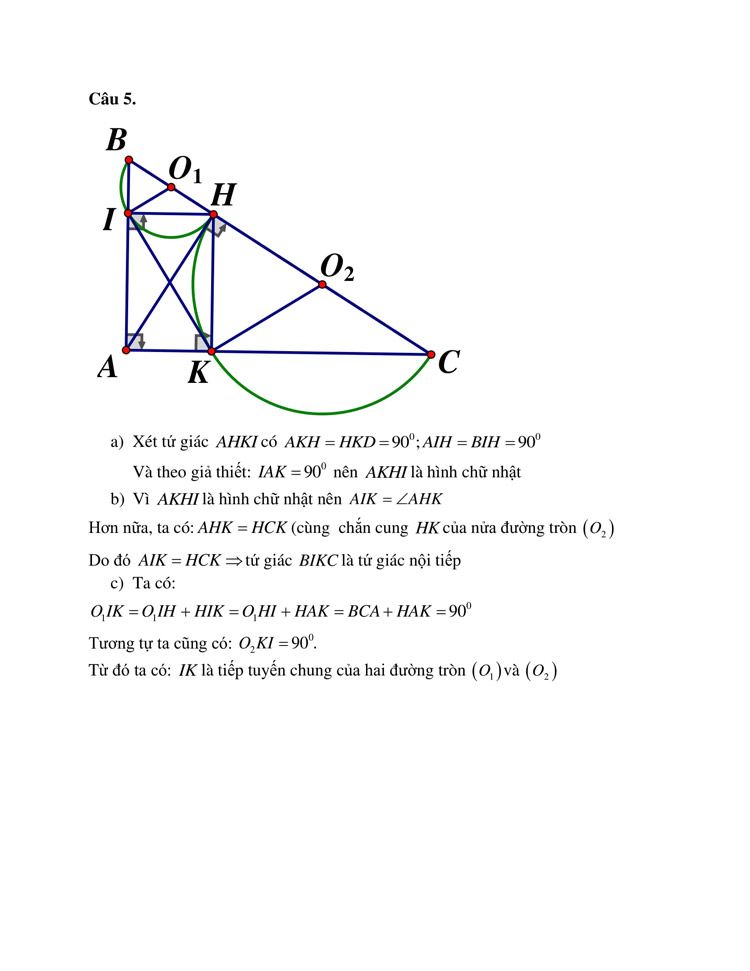
Đề thi tuyển sinh lớp 10 môn toán tỉnh Quảng Bình năm 2019
Câu 2. (1,5 điểm). Cho hàm số y=(a-2)x+5 có đồ thị là đường thẳng d
a) Với giá trị nào của a để Hàm số đồng biến trên R
b) Tìm a để đường thẳng d đi qua điểm M(2;3)
Xem chi tiết đề thi và đáp án tại link: Đề thi vào lớp 10 môn Toán tỉnh Quảng Bình năm 2019
Đề thi tuyển sinh lớp 10 môn toán tỉnh Quảng Bình năm 2013

Xem chi tiết đề thi và đáp án tại link: Đề thi vào lớp 10 tỉnh Quảng Bình năm 2013 - 2014
Trên đây là toàn bộ nội dung của đề thi tuyển sinh lớp 10 môn Toán 2023 và các năm trước của tỉnh Quảng Bình mà Đọc Tài Liệu chia sẻ nhằm giúp các em nắm được các thông tin về kỳ thi này.
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành giúp các bạn hoàn thành tốt bài thi của mình.
