Đề thi tuyển sinh lớp 10 môn Toán tỉnh Bình Định năm học 2023 - 2024 nhanh nhất cùng đáp án chi tiết. Mời các bạn xem ngay dưới đây.
>>>Đáp án đề thi vào lớp 10 môn toán Bình Định 2024
Đề thi tuyển sinh lớp 10 môn toán Bình Định 2023
Đề thi và đáp án môn Toán kỳ thi vào lớp 10 năm 2022 tại tỉnh Bình Định sẽ được Đọc Tài Liệu cập nhật ngay khi môn thi kết thúc. Tham khảo đề thi và đáp án môn Toán Bình Định các năm trước bên dưới:
ĐÁP ÁN THAM KHẢO
Bài 1.
1.
\( \left\{ \matrix{ 5x + 3y = 1 \hfill \cr x -3 y = 5 \hfill \cr} \right.⇔ \left\{ \matrix{ 6x = 6 \hfill \cr x -3 y = 5 \hfill \cr} \right.⇔ \left\{ \matrix{ x = 1 \hfill \cr y = \dfrac{-4}{3} \hfill \cr} \right. \)
Kết luận: ....

Bài 2

Bài 3.

Bài 4

Từ (3) và (4) suy ra G, H, I, D thẳng hàng
Mà \(D G \perp A G(\mathrm{cmt}) \Rightarrow D G \perp A K \Rightarrow H I \perp A K\) (đpcm).
Bài 5.

ĐỀ THI

Xem thêm thông tin:
- Tra cứu điểm thi tuyển sinh lớp 10 năm 2023 Bình Định
- Điểm chuẩn lớp 10 năm 2023 Bình Định
- Đề thi tuyển sinh lớp 10 môn Toán năm 2023
- Đề thi tuyển sinh lớp 10 môn Văn Bình Định 2023
- Đề thi tuyển sinh lớp 10 môn Anh Bình Định 2023
Đề thi tuyển sinh lớp 10 môn Toán Bình Định 2022
Bài 3: (1,5 điểm)
Tam giác vuông có cạnh huyền bằng 13cm, diện tích là 30cm2. Tính độ dài các cạnh góc vuông.
Bài 4: (3,5 điểm)
Từ một điểm S ở ngoài đường tròn (O) kẻ hai tiếp tuyến SB, SC (B, C là các tiếp điểm) và một cát tuyến cắt (O) tại D và E (D nằm giữa S và E). Qua B kẻ đường thẳng song song với DE cắt đường tròn (O) tại điểm thứ hai là A. BC và AC cắt DE lần lượt tại F và I.
a) Chứng minh: ∠SIC=∠SBC.
b) Chứng minh 5 điểm S, B, O, I, C cùng nằm trên một đường tròn.

ĐÁP ÁN
Câu 1

Câu 2


Câu 3

Câu 4


Câu 5

Trong thời gian ôn luyện, các em có thể thử sức thêm với bộ đề thi thử vào 10 môn toán Bình Định của các trường trên địa bàn tỉnh để củng cố kiến thức.
Đề thi tuyển sinh lớp 10 môn Toán tỉnh Bình Định các năm trước
Đề thi tuyển sinh lớp 10 môn toán Bình Định năm 2021

Đáp án đề thi vào 10 môn toán Bình Định 2021
Bài 1.

Bài 2.
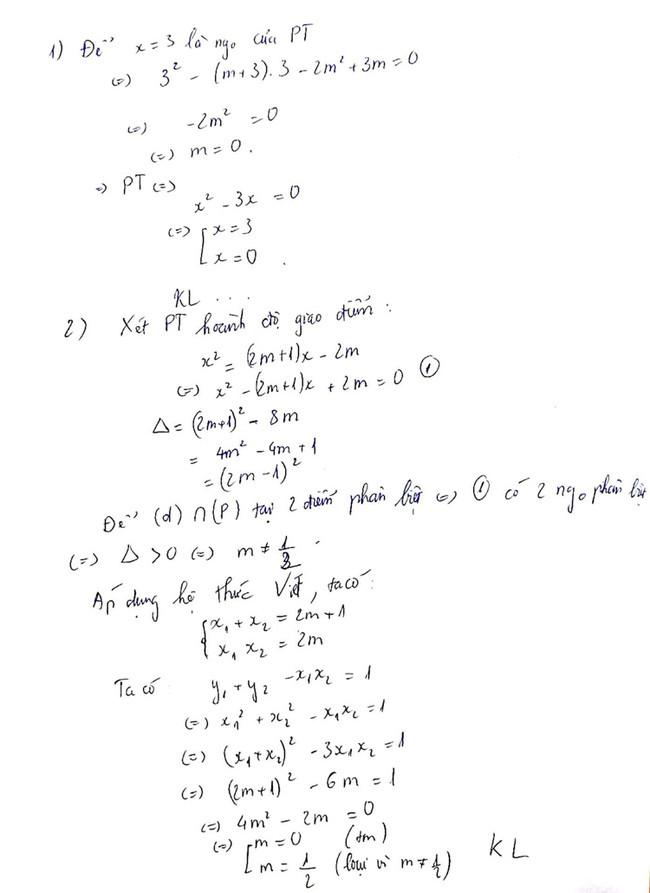
Bài 3:
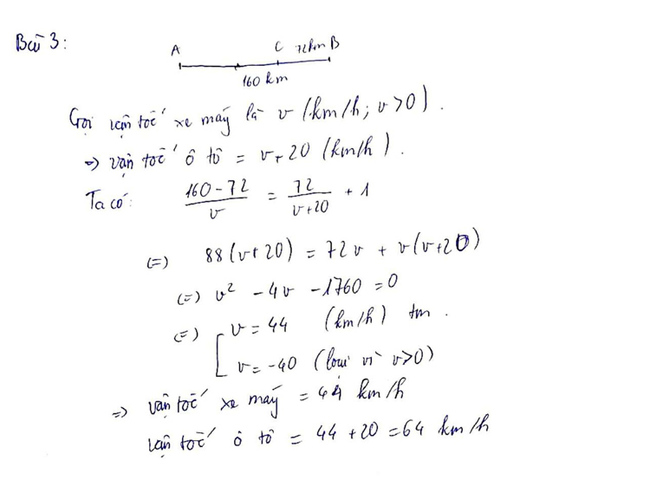
Bài 4

Bài 5. Ta có a, b, c là các số thực dương thỏa mãn
\(\begin{aligned} &\dfrac{1}{1+a}+\dfrac{1}{1+b}+\dfrac{1}{1+c}=2 \\ &\Leftrightarrow \dfrac{1}{1+a}=1-\dfrac{1}{1+b}+1-\dfrac{1}{1+c} \end{aligned}\)
\(\Leftrightarrow \dfrac{1}{1+a}=\dfrac{b}{1+b}+\dfrac{c}{1+c} \geqslant 2 \sqrt{\dfrac{b c}{(1+b)(1+c)}}( \,Bđt \, \,Cos i)\)
Tương tự
\(\begin{aligned} &\dfrac{1}{1+b} \geqslant 2 \sqrt{\dfrac{a c}{(1+a)(1+c)}} \\ &\dfrac{1}{1+c} \geqslant 2 \sqrt{\dfrac{a b}{(1+a)(1+b)}} . \end{aligned}\)
Nhân vế theo vế ta được:
\(\dfrac{1}{(1+a)(1+b)(1+c)} \geqslant 8 \dfrac{\sqrt{a^{2} b^{2} c^{2}}}{\sqrt{(1+a)^{2}(1-b)^{2}(1+c)^{2}}}=\dfrac{8 a b c}{(1+a)(1+b)(1+c)}\)
\(\Leftrightarrow \quad a b c \leqslant \dfrac{1}{8}\) => đpcm
Dấu " = " xảy ra khi a = b= c
Khi đó
\(\dfrac{3}{1+a}=2 \Rightarrow a=\dfrac{1}{2}\)
Vậy \(abc_{max}=\dfrac{1}{8} \)khi \(a=b=c=\dfrac{1}{2}\)
Đề thi tuyển sinh lớp 10 môn toán Bình Định năm 2020

Xem thêm chi tiết đáp án đề thi toán vào 10 năm 2020 tỉnh Bình Định
Đề thi tuyển sinh lớp 10 môn toán Bình Định năm 2019

Xem thêm chi tiết đáp án đề thi toán vào 10 năm 2019 tỉnh Bình Định
Đề thi tuyển sinh lớp 10 môn toán Bình Định năm 2018

Xem thêm chi tiết đáp án đề thi toán vào 10 năm 2018 tỉnh Bình Định
Trên đây là nội dung đáp án đề thi tuyển sinh vào 10 môn Toán tỉnh Bình Định qua các năm trước đó để các em đối chiếu, thử sức với các đề khác nhau. Chúc các em luôn học tốt và đạt kết quả cao trong kì thi tuyển sinh vào lớp 10.
