Bài 2.1 trang 25 sgk toán 10 tập 1 Kết nối tri thức
Câu hỏi
Bất phương trình nào sau đây là bất phương tình bậc nhất hai ẩn?
a) 2x+3y > 6
b) \({2^2}x + y \le 0\)
c) \(2{x^2} - y \ge 1\)
Bài giải
a) Ta có hệ số a=2, b=3, c=6 và các ẩn là x và y.
=> bất phương trình 2x+3y>6 là bất phương trình bậc nhất hai ẩn.
b) Ta có \({2^2}x + y \le 0 \Leftrightarrow 4x + y \le 0\)
=> a=4,b=1 và c=0. Các ẩn là x và y
=> \({2^2}x + y \le 0\) là bất phương trình bậc nhất hai ẩn.
c) \(2{x^2} - y \ge 1\) có bậc của x là 2 nên đây không là bất phương trình bậc nhất hai ẩn.
Chú ý
Khi bậc của x và y lớn hơn 1 thì bất phương trình bài cho không là bất phương trình bậc nhất hai ẩn.
Bài 2.2 trang 25 sgk toán 10 tập 1 Kết nối tri thức
Câu hỏi
Biểu diễn miền nghiệm của mỗi bất phương trình sau trên mặt phẳng tọa độ:
a) \(3x + 2y \ge 300\)
b) \(7x + 20y < 0\)
Bài giải
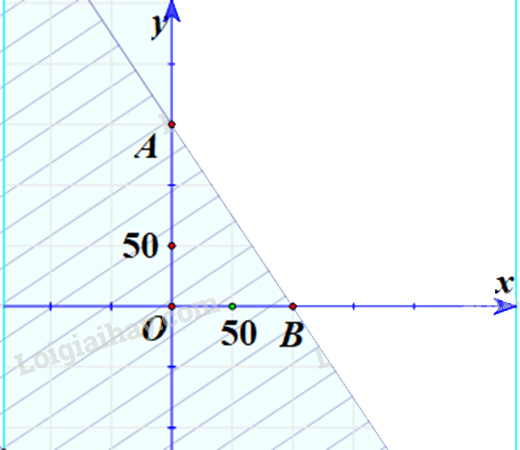
Bước 1: Vẽ đường thẳng 7x+20y=0 (nét đứt) đi qua O(0;0) và C(1;-20/7)
Bước 2: Thay tọa độ điểm A(-1;-1) vào biểu thức 7x+20y ta được:
7.(-1)+20.(-1)=-27<0
=> Điểm A thuộc miền nghiệm
=> Miền nghiệm là nửa mặt phẳng bờ là đường thẳng 7x+20y=0 và chứa điểm A(-1;-1) (không kể đường thẳng 7x+20y=0)
b)
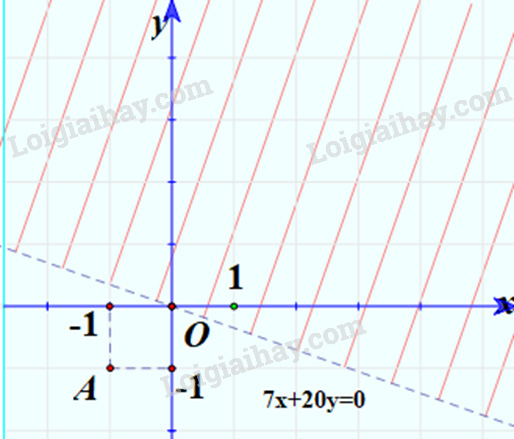
Bước 1: Vẽ đường thẳng 7x+20y=0 (nét đứt) đi qua O(0;0) và C(1;-20/7)
Bước 2: Thay tọa độ điểm A(-1;-1) vào biểu thức 7x+20y ta được:
7.(-1)+20.(-1)=-27<0
=> Điểm A thuộc miền nghiệm
=> Miền nghiệm là nửa mặt phẳng bờ là đường thẳng 7x+20y=0 và chứa điểm A(-1;-1) (không kể đường thẳng 7x+20y=0)
Bài 2.3 trang 25 sgk toán 10 tập 1 Kết nối tri thức
Câu hỏi
Ông An muốn thuê một chiếc ô tô (có lái xe) trong một tuần. Giá thuê xe được cho như bảng sau (SGK)
a) Gọi x và y lần lượt là số kilômét ông An đi trong các ngày từ thứ Hai đến thứ Sáu và
trong hai ngày cuối tuần. Viết bất phương trình biểu thị mối liên hệ giữa x và y sao cho
tổng số tiền ông An phải trả không quá 14 triệu đồng.
b) Biểu diễn miền nghiệm của bất phương trình ở câu a trên mặt phẳng toạ độ.
Bài giải
a)
Ta có 14 triệu = 14 000 (nghìn đồng)
Phí cố định là: 900.5 + 1500.2 = 7500 (nghìn đồng)
Phí tính theo quãng đường là:
x km trong các ngày từ thứ Hai đến thứ Sáu là 8x (nghìn đồng)
y km trong 2 cuối tuần là 10y (nghìn đồng)
Tổng số tiền ông An phải trả là 8x+10y +7500 (nghìn đồng)
Vì số tiền không quá 14 triệu đồng nên ta có :
\(\begin{array}{l}8x + 10y +7500 \le 14000\\ \Leftrightarrow 4x + 5y \le 3250\end{array}\)
Vậy bất phương trình cần tìm là \(4x + 5y \le 3250\)
b)
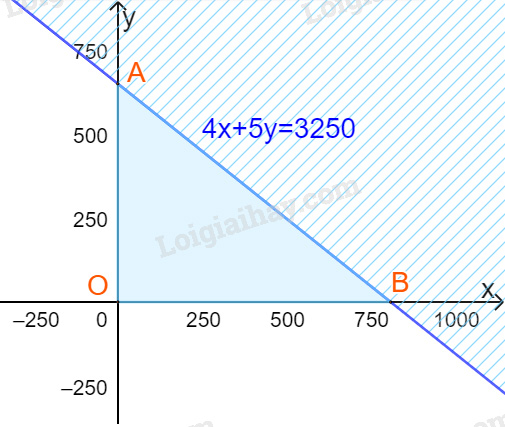
Bước 1: Vẽ đường thẳng \(4x + 5y = 3250\)(nét liền)
Bước 2: Thay tọa độ điểm O(0;0) vào biểu thức 4x+5y ta được:
4.0+5.0=0<3250
=> Điểm O thuộc miền nghiệm
=> Miền nghiệm là nửa mặt phẳng bờ là đường thẳng \(4x + 5y = 3250\) và chứa gốc tọa độ và (x;y) nằm trong miền tam giác OAB kể cả đoạn AB.
Bài tiếp theo: Trang 30 SGK Toán 10 tập 1 Kết nối tri thức
Xem thêm:
Trên đây là chi tiết hướng dẫn Giải bài tập Trang 25 SGK Toán 10 tập 1 Kết nối tri thức được Đọc Tài Liệu biên soạn với mong muốn hỗ trợ các em học sinh học tốt hơn môn Toán lớp 10
Hướng dẫn giải Toán 10 Kết nối tri thức bởi Đọc Tài Liệu