Hệ thống kiến thức lý thuyết tiết góc ở tâm, số đo cung cùng các dạng toán thường gặp cùng hướng dẫn chi tiết cách làm, qua đó giúp các em nắm được kiến thức từ khái quát đến chi tiết để học tốt phần kiến thức này.
Mời các em cùng tham khảo:

I. Lý thuyết về góc ở tâm, số đo cung
a. Góc ở tâm
Ví dụ: \( \widehat {AOB}\) là góc ở tâm
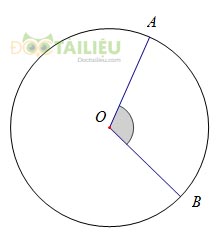
- Nếu \({0^0} < \alpha < {180^0}\) thì cung nằm bên trong góc được gọi là cung nhỏ, cung nằm bên ngoài góc được gọi là cung lớn.
- Nếu \(\alpha = {180^0}\) thì mỗi cung là một nửa đường tròn.
- Cung nằm bên trong góc được gọi là cung bị chắn. Góc bẹt chắn nửa đường tròn.
b. Số đo cung
- Số đo của cung nhỏ bằng số đo của góc ở tâm chắn cung đó.
Ví dụ: \(\widehat {AOB}\) = số đo cung AB (góc ở tâm chắn cung AB) (hình 1)
- Số đo của cung lớn bằng hiệu giữa \({360^0}\) và số đo của cung nhỏ (có chung 2 mút với cung lớn).
- Số đo của nửa đường tròn bằng \({180^0}\) . Cả đường tròn có số đo \({360^0}\). Cung không có số đo \({0^0}\) (cung có 2 mút trùng nhau).
c. So sánh hai cung
Trong một đường tròn hay hai đường tròn bằng nhau:
- Hai cung được gọi là bằng nhau nếu chúng có số đo bằng nhau.
- Trong hai cung, cung nào có số đo lớn hơn được gọi là cung lớn hơn.
d. Định lý
Nếu C là một điểm nằm trên cung AB thì
\(sđ \overparen{AB}= sđ \overparen{AC} + sđ \overparen{CB}.\)
II. Các dạng toán thường gặp
Dạng 1: Tính số đo của góc ở tâm, tính số đo của cung bị chắn. So sánh các cung.
Phương pháp:
Ta sử dụng các kiến thức sau:
- Số đo cung nhỏ bằng số đo của góc ở tâm chắn cung đó
- Số đo của cung lớn bằng hiệu giữa \({360^0}\) và số đo của cung nhỏ (có chung hai đầu mút với cung lớn).
- Số đo của nửa đường tròn bằng \({180^0}\). Cung cả đường tròn có số đo \({360^0}\).
- Sử dụng tỉ số lượng giác của một góc nhọn để tính góc.
- Sử dụng quan hệ đường kính và dây cung.
III. Bài tập
Cho hai đường thẳng xy và st cắt nhau tại O, trong các góc tạo thành có góc \(40^{\circ}\). Vẽ một đường tròn tâm O. Tính số đo của các góc ở tâm xác định bởi hai trong bốn tia gốc O.
Lời giải:
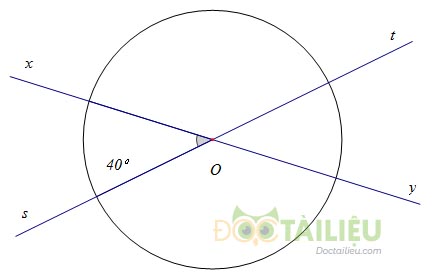
Ta có \(\widehat {xOs} = 40^\circ\) , suy ra \(\widehat {yOt} = \widehat {xOt} = 40^\circ \) (hai góc đối đỉnh)
Lại có \(\widehat {xOs} + \widehat {xOt} = 180^\circ \) (hai góc kề bù) nên \(\widehat {xOt} = 180^\circ - \widehat {xOs} = 180^\circ - 40^\circ = 140^\circ .\)
Lại có \(\widehat {sOy} = \widehat {xOt} = 140^\circ\) (hai góc đối đỉnh)
Vậy \(\widehat {xOt} = \widehat {sOy} = 140^\circ ;\,\widehat {xOs} = \widehat {tOy} = 40^\circ \)
và \(\widehat{xOy} = \widehat{sOt} = 180^{\circ}\)
=>> Xem thêm nhiều bài tập khác trong để củng cố kiến thức và rèn luyện kỹ năng làm bài
*****************
Hy vọng với hệ thống kiến thức lý thuyết góc ở tâm, số đo cung trên đây, các em sẽ có thêm một tài liệu học tập hữu ích để học tốt hơn môn Toán 9. Chúc các em luôn học tốt và đạt kết quả cao!