Bài 98 trang 105 SGK Toán 9 tập 2

Để giải bài 98 trang 105 SGK Toán 9 tập 2 không nên bỏ qua bài viết này. Với những hướng dẫn chi tiết về cách làm bài, Đọc Tài Liệu sẽ giúp các bạn đưa ra đáp án chính xác nhất và ôn tập các kiến thức trong chương trình học ôn tập chương 3 phần Hình học: Góc với đường tròn.

Đề bài 98 trang 105 SGK Toán 9 tập 2

Cho đường tròn $(O)$ và một điểm $A$ cố định trên đường tròn. Tìm quỹ tích các trung điểm $M$ của dây $AB$ khi điểm $B$ di động trên đường tròn đó.

» Bài tập trước: Bài 97 trang 105 SGK Toán 9 tập 2

Giải bài 98 trang 105 SGK Toán 9 tập 2

Hướng dẫn cách làm

+ Phần thuận: Lập luận để có $\widehat {AMO} = 90^\circ$ suy ra quỹ tích điểm $M$ là đường tròn đường kính $AO.$

+ Chứng minh phần đảo và kết luận.

Đáp án chi tiết

Dưới đây là các cách giải bài 98 trang 105 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

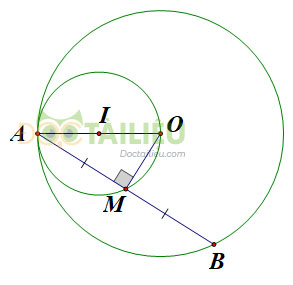
+) Phần thuận: Giả sử $M$ là trung điểm của dây $AB$. Do đó, $OM \bot AB$ hay $\widehat {AMO} = 90^\circ$. Khi $B$ di động trên đường tròn $(O)$ điểm $M$ luôn nhìn đoạn $OA$ cố định dưới một góc vuông. Vậy quỹ tích của điểm $M$ là đường tròn tâm $I$ đường kính $OA$.

+) Phần đảo: Lấy điểm $M’$ bất kì trên đường tròn $(I)$. Nối $M’$ với $A$, đường thẳng $M’A$ cắt đường tròn $(O)$ tại $B’$. Nối $M’$ với $O$, ta có $\widehat {AM'O} = {90^0}$ hay $OM’ \bot AB’$

⇒ $M$ là trung điểm của $AB’$

Kết luận: Tập hợp các trung điểm $M$ của dây $AB$ là đường tròn đường kính $OA$.

» Bài tiếp theo: Bài 99 trang 105 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 98 trang 105 Toán hình học 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.