Lời giải bài 9 trang 114 SGK toán hình học lớp 11

1. Đề bài

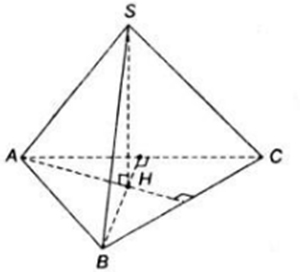
Cho hình hộp tam giác đều S.ABC có SH là đường cao. Chứng minh SA vuông góc với BC và SB vuông góc với AC.

2. Đáp án - hướng dẫn giải bài 9 trang 114

Chóp tam giác đều nên ta có H là trực tâm của tam giác ABCSH ⊥ (ABC ) ⇒ SH ⊥ BC

Và AH ⊥ BC (vì H là trực tâm)

Suy ra BC ⊥ (SAH)

SA ⊂ (SAH) ⇒ B C ⊥ S A .

Chứng minh tương tự, ta có: SH ⊥ (ABC) ⇒ SH ⊥ AC .

Mà H là trực tâm của tam giác ABC ⇒ BH ⊥ AC ⇒ AC ⊥ (SBH)

S B ⊂ ( S B H ) ⇒ A C ⊥ S B