Bài 7 trang 134 SGK Toán 9 tập 2

Đáp án bài 7 trang 134 SGK Toán 9 tập 2 được biên soạn bởi Đọc Tài Liệu nhằm mục đích tham khảo phương pháp làm bài. Tài liệu cũng giúp các bạn ôn tập nội dung kiến thức trong Toán 9 để hoàn thành bài tập ôn tập cuối năm phần hình học.

Đề bài 7 trang 134 SGK Toán 9 tập 2

Cho tam giác đều \(ABC\), \(O\) là trung điểm của \(BC\). Trên các cạnh \(AB, AC\) lần lượt lấy các điểm di động \(D\) và \(E\) sao cho góc \(\widehat {DOE} = {60^0}\).

a) Chứng minh tích \(BD.CE\) không đổi.

b) Chứng minh \(ΔBOD\) đồng dạng \(ΔOED\). Từ đó suy ra tia \(DO\) là tia phân giác của góc \(BDE\).

c) Vẽ đường tròn tâm \(O\) tiếp xúc với \(AB\). Chứng minh rằng đường tròn này luôn tiếp xúc với \(DE\).

» Bài tập trước: Bài 6 trang 134 SGK Toán 9 tập 2

Giải bài 7 trang 134 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Chứng minh các cặp tam giác bằng nhau suy ra các cạnh tương ứng bằng nhau.

+) Chứng minh các cặp tam giác đồng dạng suy ra các cặp cạnh tương ứng tỉ lệ.

Đáp án chi tiết

Dưới đây là các cách giải bài 7 trang 134 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

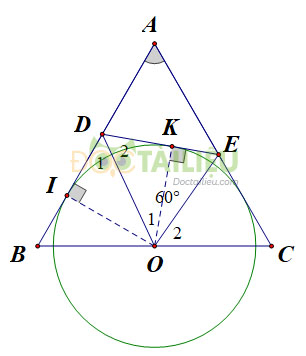
a) Chứng minh tích \(BD.CE\) không đổi.

Ta có \(\widehat {DOC}\) là góc ngoài của \(∆ BDO\) nên: \(\widehat {DOC} = \widehat B + {\widehat D_1}\)

hay \(\widehat {{O_1}} + \widehat {{O_2}} = \widehat B + \widehat {{D_1}} \Leftrightarrow {60^0} + \widehat {{O_2}} = {60^0} + \widehat {{D_1}}\)

\(\Leftrightarrow \widehat {{O_2}} = \widehat {{D_1}}\)

Xét hai tam giác: \(∆BOD\) và \(∆CEO\), ta có: \(\widehat B = \widehat C = {60^0}\) (gt)  và \(\widehat {{O_2}} = \widehat {{D_1}}\) (cmt)

\(⇒ ∆BOD\) đồng dạng \(∆CEO\) (g.g)

\( \displaystyle \Rightarrow {{B{\rm{D}}} \over {BO}} = {{CO} \over {CE}} \Rightarrow B{\rm{D}}.CE = BO.CO\)

hay \(\displaystyle B{\rm{D}}.CE = {{BC} \over 2}.{{BC} \over 2} = {{B{C^2}} \over 4}\) (không đổi)

Vậy \(\displaystyle B{\rm{D}}.CE = {{B{C^2}} \over 4}\) không đổi

b) Chứng minh \(ΔBOD\) đồng dạng \(ΔOED\)

Từ câu (a) ta có: \(∆BOD\) đồng dạng \(∆CEO\)

\( \displaystyle \Rightarrow {{O{\rm{D}}} \over {OE}} = {{B{\rm{D}}} \over {OC}} = {{B{\rm{D}}} \over {OB}}\) (do \(OC = OB\))

Mà \(\widehat B = \widehat {DOE} = {60^0}\)

Vậy \(ΔBOD\) đồng dạng \(ΔOED\) (c.g.c) \(\Rightarrow \widehat {B{\rm{D}}O} = \widehat {O{\rm{D}}E}\)

hay \(DO\) là tia phân giác của góc \(BDE\)

c) Vẽ \(OK \bot DE\) và gọi \(I\) là tiếp điểm của \((O)\) với \(AB\), khi đó \(OI \bot AB\). Xét hai tam giác vuông: \(IDO\) và \(KDO\), ta có:

\(DO\) chung

\(\widehat {{D_1}} = \widehat {{D_2}}\) (do \(DO\) là tia phân giác của góc \(BDE\))

Vậy \(ΔIDO= ΔKDO \, (ch - gn)\)\( ⇒ OI = OK\) (các cạnh tương ứng).

Điều này chứng tỏ rằng \(OK\) là bán kính của \((O)\) và \(OK \bot DE\) nên \(K\) là tiếp điểm của \(DE\) với \((O)\) hay \(DE\) tiếp xúc với đường tròn \((O).\)

» Bài tiếp theo: Bài 8 trang 134 SGK Toán 9 tập 2

Trên đây là hướng dẫn cách làm và đáp án bài 7 trang 134 Toán hình học 9 tập 2. Các em cũng có thể tham khảo thêm các bài tập tại chuyên mục giải Toán 9 của doctailieu.com.