Đáp án bài 3 trang 104 sách giáo khoa hình học lớp 11

1. Đề bài

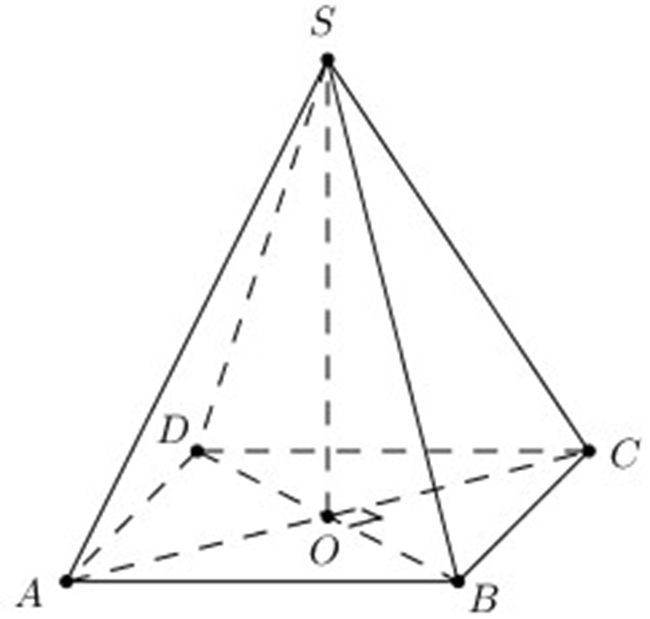
Cho hình chóp S.ABCD có đáy là hình thoi ABCD tâm O và có SA = SB = SC = SD. Chứng minh rằng:

• a) Đường thẳng SO vuông góc với mặt phẳng (ABCD)
• b) Đường thẳng AC vuông góc với mặt phẳng (SBD) và đường thẳng BD vuông góc với mặt phẳng (SAC).

2. Đáp án - hướng dẫn giải bài 3 trang 104

a) Theo giả thiết SA = SC nên tam giác SAC cân tại SO là giao của hai đường chéo hình bình hành nên O là trung điểm của AC và BD .

Do đó SO vừa là trung tuyến đồng thời là đường cao trong tam giác SAC hay SO ⊥ AC (1)

Chứng minh tương tự ta được: SO ⊥ BD (2)

Từ (1) và (2) suy ra SO ⊥ (ABCD) .

b) ABCD là hình thoi nên AC ⊥ BD (3)

Từ (1) và (3) suy ra AC ⊥ (SBD )

Từ (2) và (3) suy ra B D ⊥ ( S A C )