Bài 15 trang 135 SGK Toán 9 tập 2

Lời giải bài 15 trang 135 SGK Toán 9 tập 2 được chia sẻ với mục đích tham khảo cách làm và so sánh đáp án. Cùng với đó góp phần giúp bạn ôn tập lại các kiến thức Toán 9 ôn tập cuối năm phần hình học để tự tin hoàn thành tốt các bài tập ôn tập.

Đề bài 15 trang 135 SGK Toán 9 tập 2

Tam giác $ABC$ cân tại $A$ có cạnh đáy nhỏ hơn cạnh bên, nội tiếp đường tròn $(O).$ Tiếp tuyến tại $B$ và $C$ của đường tròn lần lượt cắt tia $AC$ và tia $AB$ ở $D$ và $E.$ Chứng minh:

a) $BD^2 = AD.CD.$

b) Tứ giác $BCDE$ là tứ giác nội tiếp.

c) $BC$ song song với $DE.$

» Bài tập trước: Bài 14 trang 135 SGK Toán 9 tập 2

Giải bài 15 trang 135 SGK Toán 9 tập 2

Hướng dẫn cách làm

+) Trong một đường tròn, góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn  một cung thì có số đo bằng nhau.

+) Trong một tứ giác, hai góc có đỉnh liên tiếp cùng nhìn một đoạn thẳng dưới một cặp góc bằng nhau thì là tứ giác nội tiếp.

Đáp án chi tiết

Dưới đây là các cách giải bài 15 trang 135 SGK Toán 9 tập 2 để các bạn tham khảo và so sánh bài làm của mình:

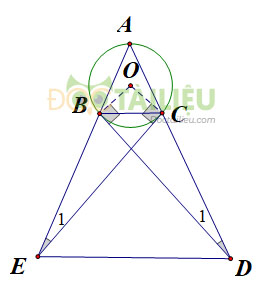
a) Xét $∆ADB$ và $∆BDC,$ ta có:

$\widehat {BA{\rm{D}}} = \widehat {CB{\rm{D}}}$ ( góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung $BC$

$\widehat {{D_1}}$ góc chung

Vậy $∆ADB$ đồng dạng $∆BDC$ ⇒ $\displaystyle {{B{\rm{D}}} \over {C{\rm{D}}}} = {{A{\rm{D}}} \over {B{\rm{D}}}} (g-g)$

$\Rightarrow B{{\rm{D}}^2} = A{\rm{D}}.C{\rm{D}}$ (đpcm)

b) Ta có $\widehat {A{\rm{E}}C}$ là góc có đỉnh ở bên ngoài $(O)$

$\displaystyle \widehat {AEC} = {sđ\overparen{AC}-sđ\overparen{BC}\over 2} = { sđ\overparen{AB}-sđ\overparen{BC}\over 2} = \widehat {ADB}$

Xét tứ giác $BCDE$, ta có: $\widehat {A{\rm{E}}C}$ và $\widehat {ADB}$ là hai góc liên tiếp cùng nhìn đoạn $BC$ và $\widehat {A{\rm{E}}C} = \widehat {ADB}$ .

Vậy tứ giác $BCDE$ nội tiếp đường tròn

c) Ta có: $\widehat {ACB} + \widehat {BC{\rm{D}}} = {180^0}$ (hai góc kề bù).

hay $\widehat {ABC} + \widehat {BC{\rm{D}}} = {180^0}$ ($∆ABC$ cân tại $A$)

$\Rightarrow \widehat {ABC} = {180^0} - \widehat {BC{\rm{D}}}(1)$

Vì $BCDE$ là tứ giác nội tiếp nên

$\widehat {BE{\rm{D}}} + \widehat {BC{\rm{D}}} = {180^0} \Rightarrow \widehat {BE{\rm{D}}} = {180^0} - \widehat {BC{\rm{D}}}(2)$

So sánh (1) và (2), ta có: $\widehat {ABC} = \widehat {BE{\rm{D}}}$

Ta cũng có: $\widehat {ABC}$ và $\widehat {BE{\rm{D}}}$ là hai góc đồng vị. Suy ra: $BC // DE$ (đpcm)

» Bài tiếp theo: Bài 16 trang 135 SGK Toán 9 tập 2

Trên đây là nội dung hướng dẫn trả lời bài 15 trang 135 SGK Toán 9 tập 2 được Đọc Tài Liệu chia sẻ để giúp bạn hoàn thành tốt bài làm của mình. Mong rằng những tài liệu giải Toán 9 của chúng tôi sẽ luôn là người bạn đồng hành để giúp bạn học tốt hơn môn học này.