Giải toán lớp 11: Đáp án bài 1 trang 77 SGK hình học

1. Đề bài

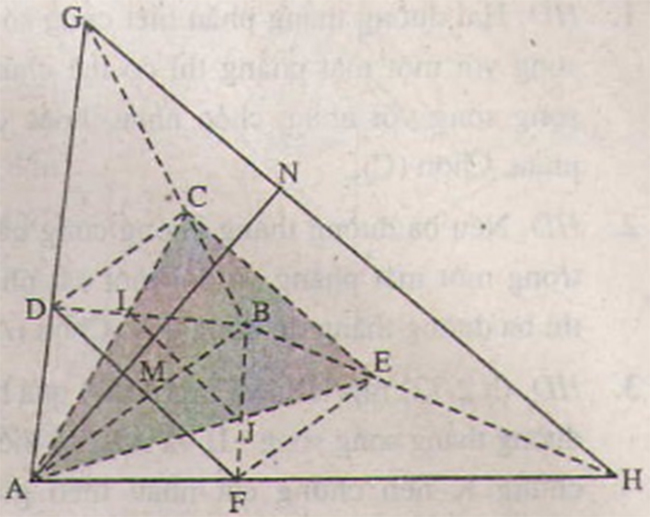
Cho hai hình thang ABCD và ABEF có chung đáy lớn AB và không cùng nằm trong một mặt phẳng.

• a) Tìm giao tuyến của các mặt phẳng sau: (AEC) và (BFD), (BCE) và (ADF).
• b) Lấy điểm M thuộc đoạn DF. Tìm giao điểm của đường thẳng AM với mặt phẳng (BCE).
• c) Chứng minh hai đường thẳng AC và BF không cắt nhau.

2. Đáp án - hướng dẫn giải bài 1 trang 77

a) Trong (ABCD) : Gọi I = AC ∩ BD

Trong (ABEF) : Gọi J = AE ∩ BF ⇒ (ACE) ∩ (BDF) = IJ .

Tương tự (BCE) ∩ (ADF) = GH

b) Trong (AGH) : Gọi N = AM ∩ GH , N ∈ AM và N ∈ GH ⊂ (BCE)

Do đó: N = AM ∩ (BCE)

c) Chứng minh bằng phương pháp phản chứng. Giả sử AC và BE cùng nằm trong một mặt phẳng, lập luận dẫn tới (ABCD) ≡ (ABEF) hay chúng cùng nằm trong một mặt phẳng (trái với giả thiết)

Do đó: A C và B F không cắt nhau.