Đề thi tuyển sinh vào lớp 10 môn Toán chung năm 2020 Chuyên Lê Hồng Phong (có đáp án) được ĐọcTàiLiệu cập nhật giúp các em học sinh tham khảo, so sánh kết quả với bài thi của mình.
Đề thi vào lớp 10 năm 2020
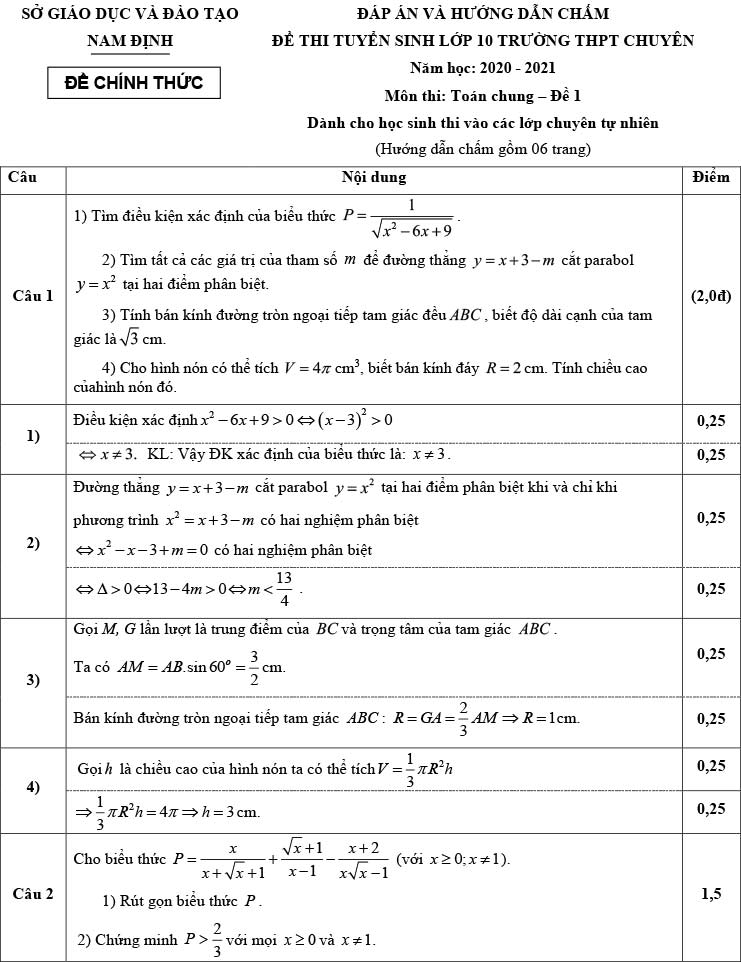
Đề số 1 - Dành cho học sinh thi vào các lớp chuyên tự nhiên

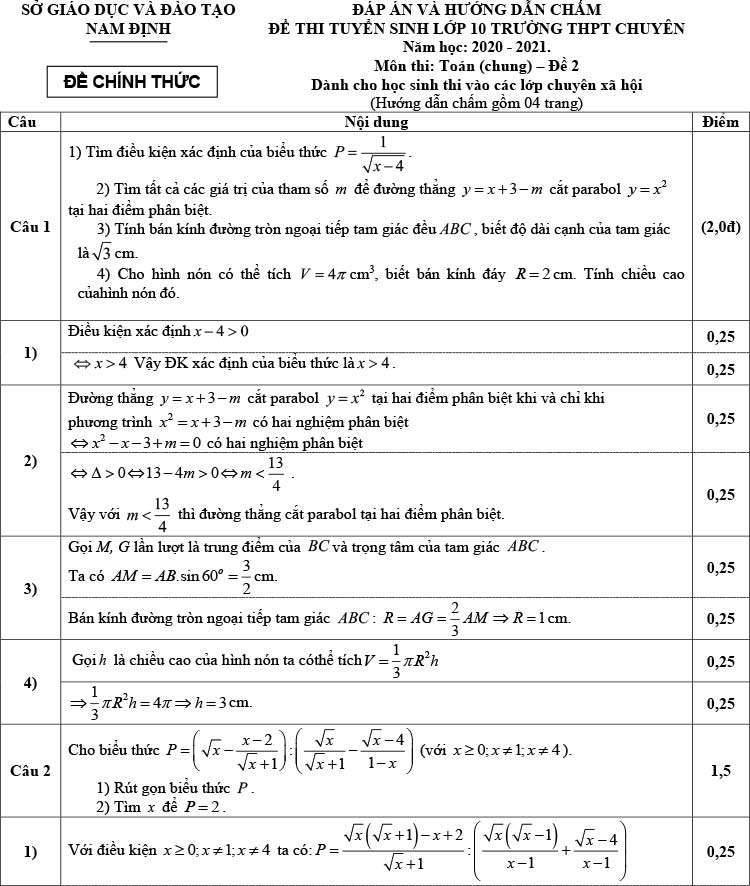
Môn thi: Toán (chung) - Đề 2 Dành cho học sinh thi vào các lớp chuyên xã hội

Đáp án đề vào lớp 10 môn Toán Chuyên Lê Hồng Phong 2020
Đáp án đề thi vào lớp 10 môn toán 2020 chuyên Lê Hồng Phong chính thức từ trường và thang điểm giúp em dễ dàng thử sức ôn thi vào 10.
Thang điểm chấm
Thang điểm chấm đề 1 toán chung vào 10 Lê Hồng Phong - Ban tự nhiên



Thang điểm chấm đề 2 toán chung vào 10 Lê Hồng Phong 2020- Ban xã hội
Đáp án môn Toán chung đề 1 vào 10 chuyên Lê Hồng Phong
Câu 1. (2,0 điểm)
1)
\(P = \dfrac{1}{\sqrt{x^2-6x+9}}\)
ĐKXĐ: \({x^2-6x+9} > 0\)
\(\Leftrightarrow (x-3)^2 > 0 \Leftrightarrow x≠ 3\)
2) Xét phương trình hoành độ giao điểm:
\(x^2 = x+ 3 -m\)
\(\Leftrightarrow x^2 - x+m -3 =0\) (*)
Để đường thẳng cắt parabol đã cho tại hai điểm phân biệt ⇔ (*) có hai nghiệm phân biệt, hay:
\(\Delta = 1 - 4m + 12 >0\)
\(\Leftrightarrow m < \dfrac{13}4\).
KL....
3)
Gọi D là trung điểm AB, ta có OD ⊥ AB.
Vì △ABC đều nên AO là phân giác của ∠BAC ⇒ ∠OAB = ∠OAC = ∠BAC /2 = 30°.
⇒ OA = 2.OD.
Áp dụng Pytago, ta có:
\({OA}^2 = {OD}^2 + {DA}^2 \)
\(\Leftrightarrow {OA}^2 = {\dfrac{OA}4}^2 + {\dfrac{AB}4}^2 \)
\(\Leftrightarrow {\dfrac{3.OA}4}^2 = {\dfrac{AB}4}^2 \)
\(\Leftrightarrow {OA}^2 = {\dfrac{AB}3}^2 =1\)
\(\Leftrightarrow OA = 1\) (cm)
KL...
4) Ta có:
\(V = \dfrac{1}3 \pi r^2h = 4\pi\)
\( \Leftrightarrow h = \dfrac{12 \pi}{\pi r^2} =\dfrac{12 }{4} = 3\) (cm)
Câu 2:
1) Với x ≥ 0, x ≠ 1 ta có:
\(P = \dfrac{x}{x+\sqrt{x}+1} + \dfrac{\sqrt{x}+1}{x-1} - \dfrac{x+2}{x\sqrt{x}-1}\)
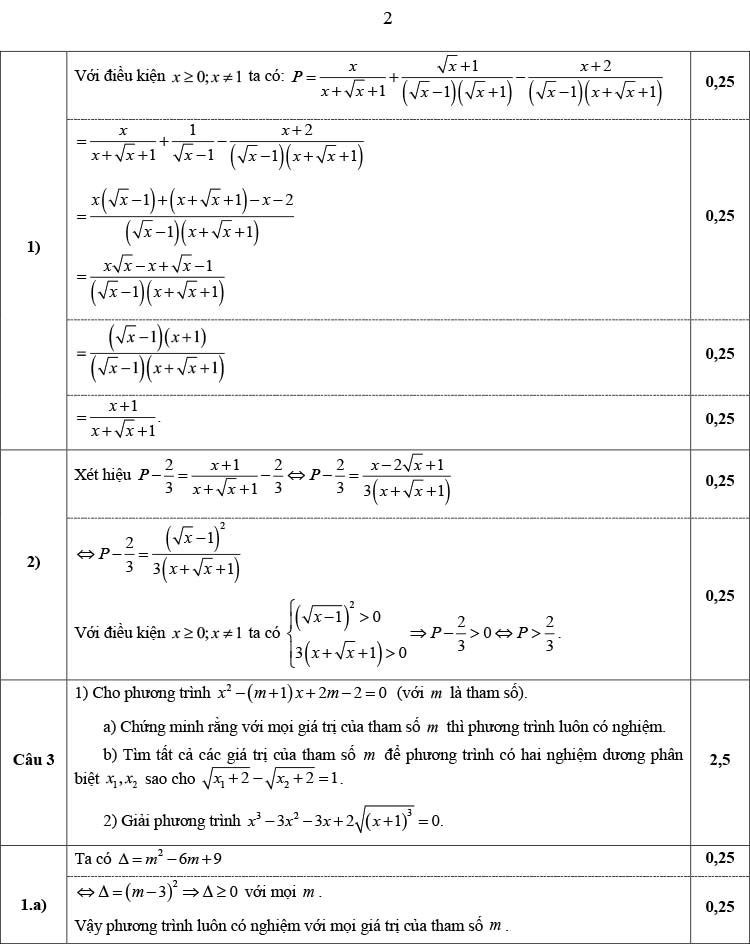
\(= \dfrac{x}{x+\sqrt{x}+1} + \dfrac{\sqrt{x}+1}{(\sqrt{x}-1)(\sqrt{x}+1)} - \dfrac{x+2}{(\sqrt{x}-1)(x+\sqrt{x}+1)}\)
\(= \dfrac{x(\sqrt{x}-1)}{(\sqrt{x}-1)(x+\sqrt{x}+1)} + \dfrac{x+\sqrt{x}+1}{(\sqrt{x}-1)(x+\sqrt{x}+1)} - \dfrac{x+2}{(\sqrt{x}-1)(x+\sqrt{x}+1)}\)
\(= \dfrac{x\sqrt{x}-x+x+\sqrt{x}+1-x-2}{(\sqrt{x}-1)(x+\sqrt{x}+1)} \)
\(= \dfrac{x\sqrt{x}-x+\sqrt{x}-1}{(\sqrt{x}-1)(x+\sqrt{x}+1)} \)
\(= \dfrac{(\sqrt{x}-1)(x+1)}{(\sqrt{x}-1)(x+\sqrt{x}+1)} \)
\(= \dfrac{x+1}{x+\sqrt{x}+1} \)
2) Với x ≥ 0, x ≠ 1 ta cần chứng minh:
\(P = \dfrac{x+1}{x+\sqrt{x}+1} > \dfrac{2}3\)
\(\Leftrightarrow 3(x+1) > 2(x+\sqrt{x}+1)\) (vì \(x+\sqrt{x}+1 >0\) với mọi x)
\(\Leftrightarrow x- 2\sqrt{x} + 1 > 0\)
\(\Leftrightarrow (\sqrt x -1)^2 > 0\) (*)
Ta thấy (*) luôn đúng với mọi x ≥ 0, x ≠ 1. Mà các phép biến đổi là tương đương nên ta có ĐPCM.
KL......
Câu 3:
1)
a)
Ta có:
\(\Delta = (m+1)^2 - 4(2m-2) = m^2 -6m + 9 = (m-3)^2 \geq 0\)
với mọi m suy ra phương trình đã cho luôn có nghiệm (đpcm).
b)
Áp dụng hệ thức Vi-ét cho phương trình đã cho, ta có:
\(\left\{ \matrix{ x_1+x_2 = m+1 \hfill \cr x_1x_2 = 2m-2 \hfill \cr} \right.\)
Để phương trình có hai nghiệm dương phân biệt ⇔
\(\left\{ \matrix{ \Delta > 0 \hfill \cr x_1+x_2 > 0 \hfill \cr x_1x_2 > 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ m ≠3 \hfill \cr m+ 1> 0 \hfill \cr 2m-2 > 0 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ m ≠3 \hfill \cr m> 1 \hfill \cr} \right.\)
Không mất tính tổng quát, giả sử \(x_1> x_2 \Leftrightarrow \sqrt{x_1+2} >\sqrt{x_2+2} \), ta có:
\(\sqrt{x_1+2} - \sqrt{x_2+2} = 1\)
\(\Leftrightarrow (\sqrt{x_1+2} - \sqrt{x_2+2})^2 = 1\)
\(\Leftrightarrow x_1+2+x_2+2 - 2\sqrt{x_1+2}. \sqrt{x_2+2} = 1\)
\(\Leftrightarrow x_1+x_2+4 - 2\sqrt{x_1x_2+2(x_1+x_2)+4}= 1\)
\(\Leftrightarrow m+1+4 - 2\sqrt{2m-2+2(m+1)+4}= 1\)
\(\Leftrightarrow m+4 = 2\sqrt{4m+4}\)
\(\Leftrightarrow (m+4)^2 = 4(4m+4)\)
\(\Leftrightarrow m^2 -8m = 0\)
\(\Leftrightarrow \left[ \matrix{ m=0 & (loại)\hfill \cr m=8 & (tm) \hfill \cr} \right.\)
KL m = 8.....
2) \(x^3 -3x^2 - 3x + 2\sqrt {(x+1)^3} = 0\)
(ĐKXĐ \(x \geq -1\))
\(\Leftrightarrow x^3 -3x(x+1) + 2(x+1)\sqrt {x+1} = 0\)
\(\Leftrightarrow x^3 -x(x+1) - 2(x+1)(x - \sqrt {x+1}) = 0\)
\(\Leftrightarrow x[x^2-(x+1)] - 2(x+1)(x - \sqrt {x+1}) = 0\)
\(\Leftrightarrow x(x + \sqrt {x+1})(x - \sqrt {x+1}) - 2(x+1)(x - \sqrt {x+1}) = 0\)
\(\Leftrightarrow [x(x + \sqrt {x+1})- 2(x+1)](x - \sqrt {x+1}) = 0\)
\(\Leftrightarrow [x^2 +x \sqrt {x+1}- 2(x+1)](x - \sqrt {x+1}) = 0\)
\(\Leftrightarrow (x -\sqrt {x+1})(x + 2\sqrt {x+1})(x - \sqrt {x+1}) = 0\)
\(\Leftrightarrow (x -\sqrt {x+1})^2(x + 2\sqrt {x+1}) = 0\)
\(\Leftrightarrow \left[ \matrix{ -x = 2\sqrt{x+1} &(1) \hfill \cr x = \sqrt {x+1} &(2) \hfill \cr} \right.\)
Ta có:
(1) \(\Rightarrow x^2 = 4(x+1)\) (với \(-1 \leq x \leq 0\))
\(\Leftrightarrow \left[ \matrix{ {x} = 2+2\sqrt 2 & (loại) \hfill \cr {x} = 2-2\sqrt 2 & (tm) \hfill \cr} \right. \)
(2) \(\Rightarrow x^2 = x+1\) (với \(x \geq 0\))
\(\Leftrightarrow \left[ \matrix{ {x} =\dfrac{1-\sqrt 5}2 & (loại) \hfill \cr {x} = \dfrac{1+\sqrt 5}2 & (tm) \hfill \cr} \right.\)
KL: PT có hai nghiệm \({x} = \dfrac{1+\sqrt 5}2\) hoặc \({x} = 2-2\sqrt 2\).
Câu 4.
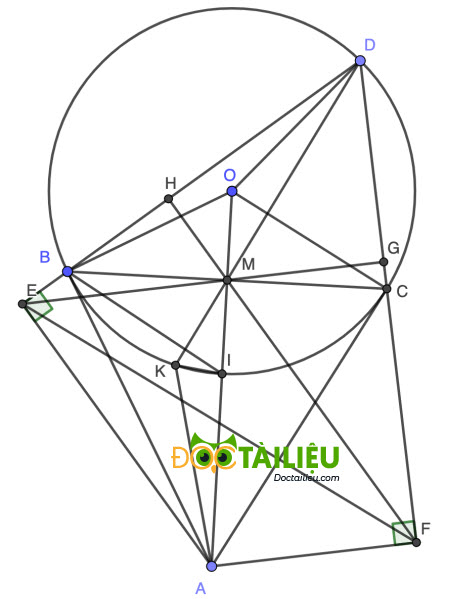
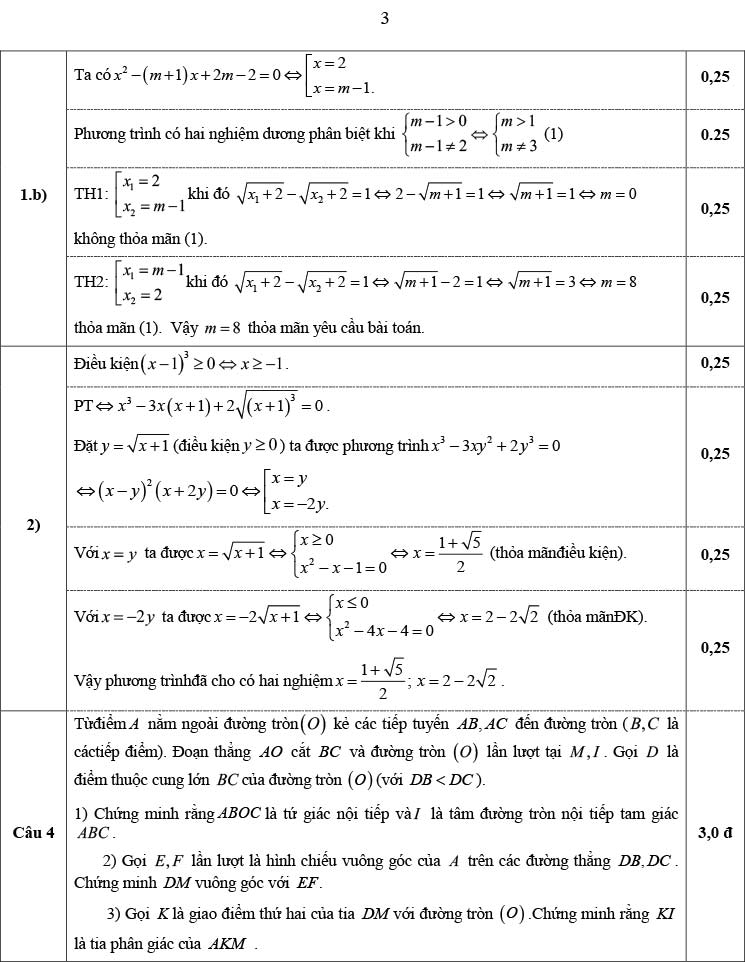
1) Vì AB, AC là tiếp tuyến tại B, C của (O) nên ∠ABO = ∠ACO = 90° ⇒ B, C cùng thuộc đường tròn đường kính OA, hay tứ giác ABOC nội tiếp (đpcm).
Theo tính chất tiếp tuyến, ta có △ABC cân tại A và AM ⊥ BC tại M ⇒ AM đồng thời là phân giác ∠BAC hay AI là phân giác ∠BAC (1)
AM đồng thời là trung trực của BC hay IM là trung trực của BC ⇒ △IBC cân tại I ⇒ ∠IBC = ∠ICB.
Lại có ∠ICB = ∠IBA (t.c góc tạo bởi tiếp tuyến và dây cung) ⇒ ∠IBC = ∠IBA ⇒ BI là phân giác ∠ABC (2)
Từ (1) và (2) suy ra I là tâm đường tròn nội tiếp tam giác ABC (đpcm).
2)
Kéo dài EM cắt DF tại G, FM cắt DB tại H.
Dễ thấy ∠AEB = ∠AMB = 90° ⇒ Tứ giác AMBE nội tiếp ⇒ ∠BEM = ∠BAM (góc nội tiếp cùng chắn cung BM) = ∠BCO (do tứ giác ABOC nội tiếp)
hay \(∠DEG =∠BCO = 90 ° -\dfrac{∠BOC}2 = 90 ° - ∠BDC\)
⇒ ∠DEG + ∠BDC = 90° ⇒ ∠EGD = 90° ⇒ EG ⊥ DF.
Tương tự ta có FH ⊥ DE.
Xét △DEF có EG ⊥ DF, FM ⊥ DE và EG cắt FH tại M ⇒ M là trực tâm của △DEF ⇒ DM ⊥ EF (đpcm).
3)
Xét △MKB và △MCD ta có:
∠KMB = ∠CMD (góc đối đỉnh)
∠MBK = ∠CBK = ∠CDK = ∠MDC
Suy ra △MKB ∽ △MCD ⇒ \(\dfrac{MK}{MB} = \dfrac{MC}{MD} \) ⇒ MK.MD = MB.MC = MB² (3)
Áp dụng hệ thức lượng trong △CBA vuông tại B có BM ⊥ CA ⇒ MO.MA = MB² (4)
Từ (3) và (4) ⇒ MK.MD = MO.MA ⇒ \(\dfrac{MK}{MA} = \dfrac{MO}{MD} \).
Xét △MKA và △MOD ta có:
∠KMA = ∠OMD (góc đối đỉnh)
\(\dfrac{MK}{MA} = \dfrac{MO}{MD} \) (cmt)
Suy ra △MKA ∽ △MOD ⇒ ∠AKM = ∠MOD = ∠IOD = 2.∠IKD
Hay ∠AKM = 2.∠IKM hay KI là phân giác của ∠AKM (đpcm).
Câu 5.
1)
\(\left\{ \matrix{ x^2(y+1) + 3x + 1 = x^2 \sqrt{1-y} & (1) \hfill \cr x^2 + 9 = 6x \sqrt{1-y} - \sqrt{x - 1}& (2) \hfill \cr} \right.\)
(ĐKXĐ: \(y \leq 1; x\geq 1\))
Đặt \(\sqrt{1-y} = a\) (a ≥ 0)
\(\Leftrightarrow y = 1-a^2\)
Ta có:
(1) \(\Leftrightarrow 3x+1 = x^2 (\sqrt{1-y}-y-1 )\)
\(\Leftrightarrow 3x+1 = x^2 (a^2+a-2 ) =x^2(a-1)(a+2)\)
\(\Leftrightarrow \dfrac{3}{x}+ \dfrac{1}{x^2} =(a-1)(a+2)\)
\(\Leftrightarrow \dfrac{1}{x}(3+ \dfrac{1}{x}) =(a-1)(a+2)\)
\(\Leftrightarrow (\dfrac{1}x+1 - 1)( \dfrac{1}{x}+1 + 2) =(a-1)(a+2)\) (*)
Đặt \(\dfrac{1}x + 1 = b\) (2 ≥ b > 1) \(\Leftrightarrow x = \dfrac{1}{b-1}\)
Ta có:
(*) \(\Leftrightarrow (b - 1)(b + 2) =(a-1)(a+2)\)
\(\Leftrightarrow b^2 - a^2 +b-a = 0\)
\(\Leftrightarrow (b-a)(b+a+1) = 0\)
Vì a ≥ 0 và 2 ≥ b > 1 ⇒ b + a + 1 > 0
\(⇒ b = a \Leftrightarrow \dfrac{1}x + 1 = \sqrt {1-y}\), thay vào (2), ta có:
\( x^2 + 9 = 6x (\dfrac{1}x+1) - \sqrt{x - 1}\)
\(\Leftrightarrow x^2 + 9 = 6 + 6x - \sqrt{x - 1}\)
\(\Leftrightarrow x^2 -6x + 3 + \sqrt{x - 1} = 0\)
\(\Leftrightarrow (x-1)^2 -4(x-1) + \sqrt{x - 1} -2= 0\)
\(\Leftrightarrow (x-1)[(x-1) -4] + \sqrt{x - 1} -2= 0\)
\(\Leftrightarrow (\sqrt{x - 1} -2) [(x-1)(\sqrt{x - 1} +2) + 1]= 0\)
Vì x ≥ 1 \(\Leftrightarrow (x-1)(\sqrt{x - 1} +2) + 1 >0\)
\(\Rightarrow \sqrt {x-1} = 2\)
\(\Leftrightarrow x = 5\) (tm đkxđ)
\(⇒ \sqrt {1-y} = \dfrac{1}x + 1 =\dfrac{6}5\)
\(\Leftrightarrow y = \dfrac{-11}{25}\)
.KL: \((x;y) = (5;\dfrac{-11}{25})\).
2)
Ta có:
\(a^2+ab+b^2 \geq \dfrac{3}4(a+b)^2\)
\(\Leftrightarrow 4(a^2+ab+b^2) \geq 3(a+b)^2\)
\(\Leftrightarrow a^2- 2ab+b^2 = (a-b)^2 \geq 0\) luôn đúng
Suy ra (*) luôn đúng.
\(\Leftrightarrow \sqrt{a^2+ab+b^2} \geq \sqrt{\dfrac{3}4(a+b)^2} =\dfrac{\sqrt 3}2(a+b) \) (**)
Áp dụng BĐT (**) cho P, ta có:
\(P = \sqrt{a^2 + ab + b^2} + \sqrt{b^2 + bc + c^2} + \sqrt{c^2 + ac + a^2} \geq \dfrac{\sqrt 3}2 (a+b+b+c+c+a)\)
\(\Leftrightarrow P \geq \sqrt 3 (a+b+c)\) (1)
Áp dụng BĐT Cauchy-Schwarz ta có:
\((\sqrt{a+1} + \sqrt{b+1} + \sqrt{c+1} )^2 \leq 3(a+1+b+1+c+1)\)
\(\Leftrightarrow 6^2 \leq 3(a+b+c+3)\)
\(\Leftrightarrow a+b+c \geq 9\) (2)
Từ (1) và (2) suy ra:
\(\Leftrightarrow P \geq \sqrt 3 (a+b+c) \geq 9\sqrt 3\)
Vậy \(min_P = 9\sqrt 3 \Leftrightarrow a=b=c= 3\).
Đang cập nhật tiếp
Đáp án môn Toán chung đề 2 vào 10 chuyên Lê Hồng Phong
Câu 1: (2.0 điêm)
1) ĐKXĐ: x > 4
2) Giao điểm của y = x + 3 - m cắt \(y = x^2\) sẽ là nghiệm của phương trình
\(x^2 = x + 3 - m\)
⇔ \(x^2 - x - 3 + m = 0\) (*)
Để (*) có 2 nghiệm phân biệt
⇔\( △ = (-1)^2 - 4.1.(m-3)>0\)
⇔ \(m < \dfrac{13}{4}\)
3. Cách 2 so với đề 1. Gọi O là tâm đường tròn ngoại tiếp và M là trung điểm BC => O đồng thời là trọng tâm tam giác ABC.
=> R = OA = 2/3 AM theo t/c trọng tâm
Mà AM = \(\dfrac{\sqrt{3}.\sqrt{3}}{2} = \dfrac{3}{2}\) (trung tuyến tam giác đều)
=> R = 1
4 . Tương tự câu 3 đề 1
Câu 2
1. \(P = \left(\sqrt{x}- \dfrac{x-2}{\sqrt{x}+1}\right) : \left(\dfrac{\sqrt{x}}{\sqrt{x}+1} - \dfrac{\sqrt{x}-4}{1-x}\right)\) với x ≥ 0; x ≠ 1, x ≠ 4
\(P = \left(\dfrac{\sqrt{x}.({\sqrt{x}+1})- x+2} {\sqrt{x}+1}\right) : \left(\dfrac{\sqrt{x}.(\sqrt{x}-1) + \sqrt{x}-4}{(\sqrt{x}-1)(\sqrt{x}+1)}\right)\)
\(P = \dfrac{\sqrt{x}+2} {\sqrt{x}+1}: \dfrac{x-4}{(\sqrt{x}-1)(\sqrt{x}+1)} = \dfrac{\sqrt{x}-1} {\sqrt{x}-2}\)
2. P = 2 ⇔ \(\dfrac{\sqrt{x}-1} {\sqrt{x}-2} = 2\) với x ≥ 0; x ≠ 1, x ≠ 4
=> \(\sqrt{x}-1 = 2 (\sqrt{x}-2) ⇔ \sqrt{x} = 3 => x = 9 (t/m)\)
Câu 3.
1. Phương trình \(x^2 - 2 (m+1)x+m^2-2m-3=0 \)
a. Khi x = 2
=> \(2^2 - 2 (m+1).2 + m^2-2m-3 = 0\)
⇔ \(m^2 - 6m - 3 = 0\)
⇔ \(m = 3 ± 2\sqrt{3}\)
b. Để \(x^2 - 2 (m+1)x+m^2-2m-3=0 \) có 2 nghiệm phân biệt \(x_1, x_2\) thì △' > 0
\(△' = (m+1)^2 - 1.(m^2-2m-3) = 4m +5\)
△' > 0 ⇔ m>-5/4
Áp dụng viet ta có:
\(\left\{ \matrix{ x_1 + x_2 = 2(m+1) \hfill \cr x_1 . x_2 = m^2 - 2m - 3\hfill \cr} \right.\)
Theo bài cho
\(x_1^2 + x_2^2 - x_1 - x_2 = 8 ⇔ (x_1+x_2)^2-2x_1x_2-(x_1+x_2)=8\)
\(⇔ 4(m+1)^2 - 2.(m^2 - 2m - 3)-2(m+1) = 8\)
\(⇔\left[ \begin{align}& m=0 \,\,(t/m)\\& m=-5 \,\,(loại)\\\end{align} \right.\\ \)
KL:____
2) \( \left\{ \matrix{ \dfrac{x}{\sqrt {x+1}+1} + \sqrt{y-2} = 4 \hfill \cr \dfrac{3x}{\sqrt {x+1}+1} - 2 \sqrt{y-2} = -3 \hfill \cr} \right.\)
(đkxđ: \(x\geq -1\))
\(\Leftrightarrow \left\{ \matrix{ \dfrac{x}{\sqrt {x+1}+1} =1 \hfill \cr \sqrt{y-2} =3 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x = \sqrt {x+1}+1 \hfill \cr y = 11 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ x +1 - \sqrt {x+1}-2 = 0 \hfill \cr y = 11 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ (\sqrt {x+1} +1)(\sqrt {x+1}-2) = 0 \hfill \cr y = 11 \hfill \cr} \right.\)
\(\Leftrightarrow \left\{ \matrix{ \sqrt {x+1}-2 = 0 \hfill \cr y = 11 \hfill \cr} \right.\) (vì \(\sqrt {x+1} +1 \geq 1 >0\))
\(\Leftrightarrow \left\{ \matrix{ x = 3 \hfill \cr y = 11 \hfill \cr} \right.\)
Câu 4:
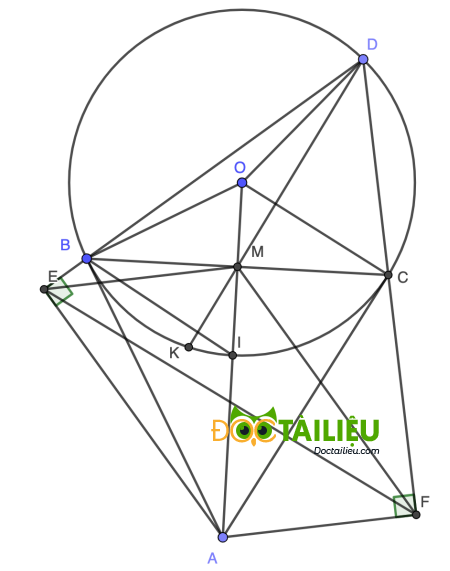
1)
Vì AB, AC là tiếp tuyến tại B, C của (O) nên ∠ABO = ∠ACO = 90° ⇒ B, C cùng thuộc đường tròn đường kính OA, hay tứ giác ABOC nội tiếp (đpcm).
Theo tính chất tiếp tuyến, ta có △ABC cân tại A và AM ⊥ BC tại M ⇒ AM đồng thời là phân giác ∠BAC hay AI là phân giác ∠BAC (1)
AM đồng thời là trung trực của BC hay IM là trung trực của BC ⇒ △IBC cân tại I ⇒ ∠IBC = ∠ICB.
Lại có ∠ICB = ∠IBA (t.c góc tạo bởi tiếp tuyến và dây cung) ⇒ ∠IBC = ∠IBA ⇒ BI là phân giác ∠ABC (2)
Từ (1) và (2) suy ra I là tâm đường tròn nội tiếp tam giác ABC (đpcm).
2)
Xét △MKB và △MCD ta có:
∠KMB = ∠CMD (góc đối đỉnh)
∠MBK = ∠CBK = ∠CDK = ∠MDC
Suy ra △MKB ∽ △MCD ⇒ \(\dfrac{MK}{MB} = \dfrac{MC}{MD} \) ⇒ MK.MD = MB.MC = MB² (3)
Áp dụng hệ thức lượng trong △CBA vuông tại B có BM ⊥ CA ⇒ MO.MA = MB² (4)
Từ (3) và (4) ⇒ MK.MD = MO.MA (đpcm).
3)
Ta có ∠ABC = ∠BDC (t.c góc tạo bởi tia tiếp tuyến và dây cung)
Dễ thấy ∠AEB = ∠AMB = 90° ⇒ Tứ giác AMBE nội tiếp ⇒ ∠EMA = ∠EBA (góc nội tiếp cùng chắn cung EA) = 180° - ∠ABD = 180° - ∠ABC - ∠CBD = 180° - ∠BDC - ∠CBD = ∠BCD
hay ∠EMA = ∠BCD.
Ta lại có ∠AFC = ∠AMC = 90° ⇒ Tứ giác AMCF nội tiếp ⇒ ∠MAF + ∠MCF = 180° ⇒ ∠MAF = 180° - ∠MCF = ∠MCD = ∠BCD
Suy ra ∠MAF = ∠EMA (cùng = ∠BCD) ⇒ EM // AF (góc ở vị trí đồng vị) (đpcm).
Câu 5:
1)
\((x^2+x)\sqrt{2x+3} = x^3 + 3x^2 + x - 2\)
(ĐKXĐ: \(x\geq -\dfrac{3}2\))
\(\Leftrightarrow (x^2+x)(\sqrt{2x+3} - x-1) = x^3 + 3x^2 + x - 2 - (x^2+x)(x+1)\)
\(\Leftrightarrow (x^2+x)(\sqrt{2x+3} - x-1) = x^2 - 2\)
\(\Leftrightarrow (x^2+x)(\sqrt{2x+3} - x-1) = (x+1)^2 - (2x+3)\)
\(\Leftrightarrow [ (x+1) - \sqrt{2x+3}][ (x+1) + \sqrt{2x+3} +x^2+x ]=0\)
Dễ thấy \((x+1) + \sqrt{2x+3} +x^2+x >0 \) với mọi \(x\geq -\dfrac{3}2\) suy ra:
\(\Leftrightarrow (x+1) - \sqrt{2x+3}=0\)
\(\Leftrightarrow (x+1) = \sqrt{2x+3}\)
\(\Leftrightarrow \left\{\begin{matrix} x+1 ≥ 0\\ 2x+3≥ 0\\ 2x+3 = (x+2)^2 \end{matrix}\right.\Leftrightarrow x= \sqrt{2}\)
KL....
2)
Áp dụng BĐT Cauchy-Swcharz ta có:
\((a+b+c)^2 \geq 3(ab+bc+ca) = 3[24- 2(a+b+c)]\)
\(\Leftrightarrow (a+b+c)^2 +6(a+b+c) - 72 \geq 0\)
\(\Leftrightarrow (a+b+c-6)(a+b+c+12) \geq 0\)
\(\Leftrightarrow a+b+c \geq 6\)
(Vì a,b,c dương)
\(\Leftrightarrow a+b+c+2 \geq 8\)
\(\Leftrightarrow (a+b+c+2)^2 \geq 64\)
Ta có:
\(P = a^2 + b^2 + c^2 = (a+b+c)^2 - 2(ab+bc+ca)\)
\(= (a+b+c)^2 - 2[24 - 2(a+b+c)] = (a+b+c)^2 + 4(a+b+c) - 48\)
\(= (a+b+c + 2)^2- 52 \geq 64 -52 =12\)
Vậy \(Min_P = 12 \Leftrightarrow a=b=c =2\).
-/-
Các môn thi khác
• Đề thi vào lớp 10 môn Văn chung năm 2020 Chuyên Lê Hồng Phong
Có thể các em quan tâm:
Trên đây là toàn bộ nội dung của đáp án đề thi tuyển sinh vào lớp 10 môn Toán năm 2020 chung đối với các thí sinh thi vào Chuyên Lê Hồng Phong (Nam Định) được Đọc Tài Liệu thực hiện sau khi kì thi chính thức diễn ra. Với nội dung này các em có thể so sánh đối chiếu kết quả bài thi của mình!
Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành hữu ích với bạn trong kỳ thi này.
