Đáp án đề thi chuyên Toán vào 10 Hà Nội năm 2021

Đáp án đề thi tuyển sinh vào lớp 10 chuyên toán năm học 2021 - 2022 của tỉnh Hà Nội được Đọc tài liệu cập nhật nhanh nhất!

Đề thi chuyên Toán vào 10 Hà Nội năm 2021

Đáp án đề thi chuyênToán vào 10 Hà Nội năm 2021

Bài 1.

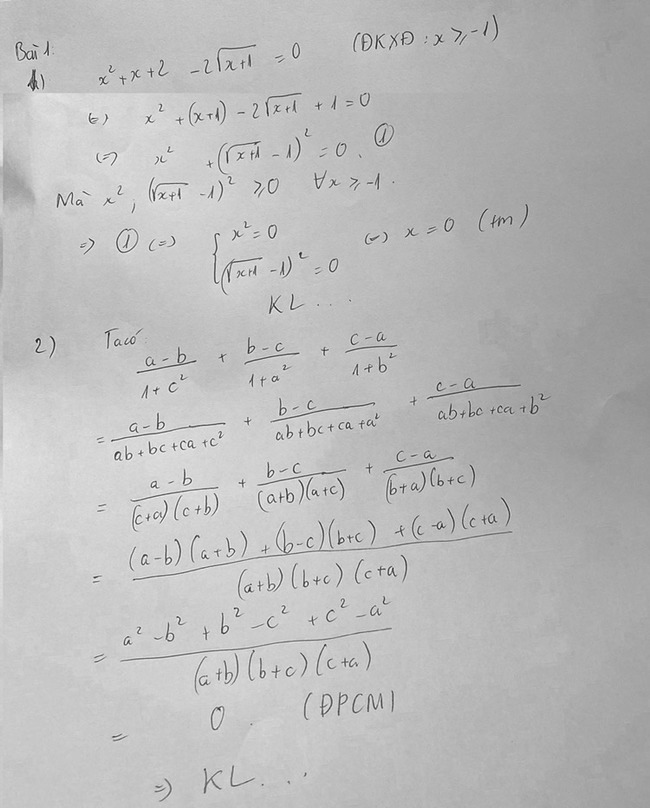
Bài 2

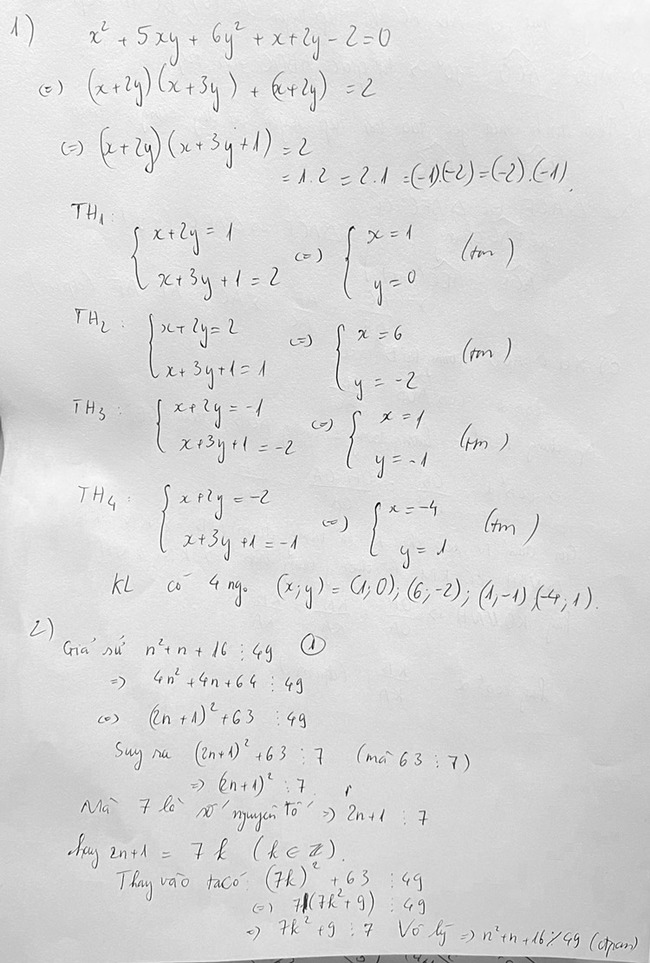
Bài 3

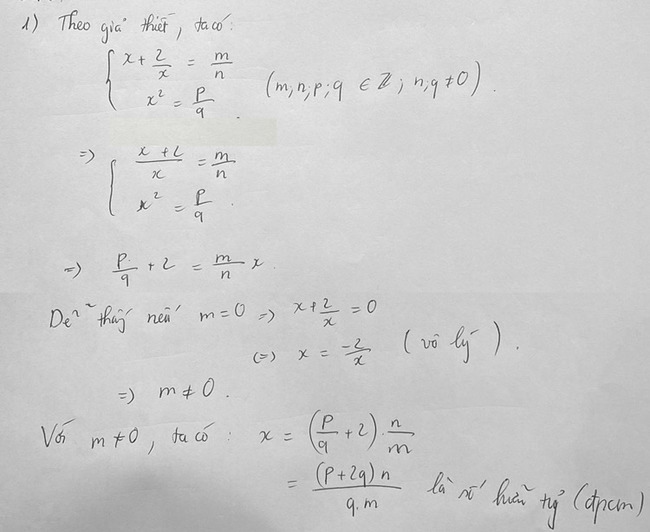
2)

Theo giả thiết ta có a, b, c không âm và a+b+c=5.

Ta dễ có \((x+y)^{2}-4 x y=(x-y)^{2} \geq 0 \).

Suy ra \(x y \leq \frac{(x+y)^{2}}{4}\) vói mọi \(x, y \in R\)

Áp dụng bất đẳng thức này, ta được:

\(\begin{aligned} 2a+2ab + abc = a(2+b(2+c) \\ &\leq a\left(2+\frac{(b+c+2)^{2}}{4}\right) \\ &=(5-b-c)\left(2+\frac{(b+c+2)^{2}}{4}\right) \end{aligned}\)

Đặt \(t=b+c(t \geq 0)\). Ta cần chứng minh:

\((5-t)\left(2+\dfrac{(t+2)^{2}}{4}\right) \leq 18\)

Thật vậy, bất đẳng thức này tương đương với

\((t-5)\left(2+\dfrac{(t+2)^{2}}{4}\right)+18 \geq 0\)

Hay,

\((t-2)^{2}(t+3) \geq 0\)

Bất đẳng thức này đúng do \( (t \geq 0)\). Suy ra

\(2 a+2 a b+a b c \leq(5-t)\left(2+\frac{(t+2)^{2}}{4}\right) \leq 18\)

Dấu bằng xảy ra khi t=2, a=3, b=2 và c=0.

Vậy ta có điều phải chứng minh.

Bài 4. Nguồn: CLB Toán Lim.

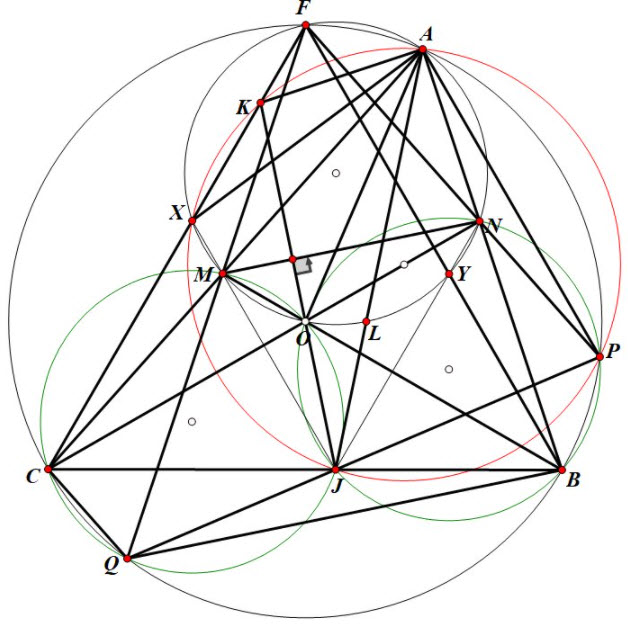
1) Ta có: \(\angle M O N=\angle B O C=2 \angle B A C=120^{\circ} \)do đó: A, M, O, N cùng thuộc 1 đường tròn.

Từ đó: CM.CA= CO.CN và BM.BO=B N.B A.

Do đó: \(C M=\dfrac{C N . C O}{C A}\) và \(B N=\dfrac{B M \cdot B O}{B A}\).

Ta cần: BN=  CM.

Như vậy cần có:\( \dfrac{C N}{C A}=\dfrac{B M}{B A}\) hay là: \(\sin \angle A N O=\sin \angle A M O\)( đúng).

2) Từ 1) ta có: △FNB=△FMC do đó: NB=MC=FN=FM dẫn đến: A P // F B.

Tương tự: AQ // FC. Do đó: CQBP là hình thang cân.

Gọi \((\operatorname{COM}) \cap(B O N)=O, J^{\prime}\).

Ta có: \(\angle O J^{\prime} C+\angle O J^{\prime} B=\angle O M A+\angle O N A=180^{\circ}\)

do đó: J', B, C thẳng hàng.

Ta có: \(\angle C Q M=\angle F B C=60^{\circ}=\angle M O C\) do đó: M, O, J', Q, C đồng viên dẫn đến: \(\angle Q \cdot J^{\prime} C=\angle C M Q\) .

Tương tự thì: \(\angle P J^{\prime} B=\angle F N A=\angle F M A= \angle C M Q\) suy ra: Q, J' P thẳng hàng.

Do đó: J trùng J'

Lại có: \(B N \cdot B A=B O \cdot B M=B J \cdot B C\) suy ra: ANJC nội tiếp dẫn đến: \(\angle J A B= \angle O C B\).

Tương tự thì: ∠JAC=∠OBC suy ra: A J là phân giác góc B A C .

3) Ta có: ∠COJ=∠B và ∠OJM= ∠OCA suy ra: ∠COJ+∠MJO=90⁰ suy ra: \(O C \perp J M.\)

Tương tự: \(O B \perp J N\). Do đó: \(J O \perp M N\).

Ta có:\( \angle A P_{d}=180^{\circ}-\angle A C Q\).

Gọi \((A M N) \cap F C=X \neq F\), ta có: \(C X \cdot C F=C O \cdot C N=C J . C B \)dẫn đến: FXJB nội tiếp suy ra: \(\angle A X J=120^{\circ}-\angle F X A=120^{\circ}-\angle F N A\) do đó: \(\angle A P J+\angle A X J=180^{\circ}\)

tức là: A, P, J, X đồng viên.

Cộng góc đơn giản ta có: J, X, M thẳng hàng.

Tương tự: J, Y, N thẳng hàng với \(Y=(A M N) \cap F B \neq F.\)

Cùng từ 2) ta có: \(\angle A J N=\angle A C O=\angle M J O\) dẫn đến: AJ đi qua tâm của FMN là L.

Do đó: \(\angle L A X=\angle L M J=\angle O J N=\angle O B A=\angle C K J\).

Do đó: A, K, X, J, P đồng viên.

Vậy tức là: AKJP nội tiếp dẫn đến: \(\angle J K A=\angle B N M\left(=180^{\circ}-\right. \angle A P J )\) dẫn đến: \(K A \perp A B.\)

Bài 5:

1. Giả sử phần tử A không chứa 2 số tự nhiên liên tiếp nào

⇒ Khoảng cách giữa 2 số gần nhau nhất tối thiểu = 2.

⇒ Khoảng cách giữa số nhỏ nhất và lớn nhất tối thiểu = 2 * (100 - 1) = 198

⇒ Số lớn nhất ≥ 198

mà A chỉ gồm các phần tử của tập hơn {1,2,3,...,178}

⇒ Điều giả sử là vô lý

⇒ A chứa hai số tự nhiên liên tiếp (ĐPCM)

Tuyển tập đề thi tuyển sinh lớp 10 môn Toán tất cả các tỉnh thành trên cả nước.

Trên đây là toàn bộ nội dung của đề thi tuyển sinh vào lớp 10 môn toán chuyên 2021 tại Hà Nội được Đọc Tài Liệu chia sẻ.

Mong rằng những tài liệu của chúng tôi sẽ là người đồng hành giúp các bạn hoàn thành tốt bài thi của mình.