Đề thi chính thức :
| SỞ GIÁO DỤC VÀ ĐÀO TẠO THÀNH PHỐ HỒ CHÍ MINH |
KÌ THI TUYỂN SINH LỚP 10 TRUNG HỌC PHỔ THÔNG NĂM HỌC 2018 - 2019 MÔN THI: TOÁN CHUYÊN |
| ĐỀ CHÍNH THỨC (Đề thi có 01 trang) |
Ngày thi: 03 tháng 6 năm 2018 Thời gian làm bài: 150 phút (không kể thời gian phát đề) |
Câu 1. (1 điểm)
Cho \(a, b,c\) là ba số thực thỏa điều kiện \(a+b+c=0\) và \(a^2 = 2(a+c+1)(a+b-1)\).
Tính giá trị của biểu thức:\( A= a^2 + b^2 +c^2 \)
Câu 2. (2 điểm)
a) Giải phương trình: \( 4\sqrt{x+3} =1+ 4x+ {2\over x}\)
b) Giải hệ phương trình: \(\left\{ {_{x^2 + y^5 = x^3 + y^3}^{x^2 + y^3 = 1}} \right.\)
Câu 3. (2 điểm)
Cho tam giác ABC (AB < AC) vuông tại A có đường cao AH. Gọi E,F lần lượt là hình chiếu của H lên AB, AC.
a) Chứng minh rằng: \(BE\sqrt {CH} +CF\sqrt {BH} = AH \sqrt {BC}\)
b) Gọi D là điểm đối xứng của B qua H và gọi O là trung điểm của BC. Đường thẳng đi qua D và vuông góc với BC cắt AC tại K. Chứng minh rằng: BK vuông góc với AO.
Câu 4. (1,5 điểm)
a) Chứng minh rằng \(x^4 - x + {1\over2}\) > 0 với mọi số thực \(x\).
b) Cho\( x, y\) là các số thực thỏa mãn điều kiện \(x^2 - xy + y^2 = 3. \)Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức \(P =x^2+y^2 \)
Câu 5. (1,5 điểm)
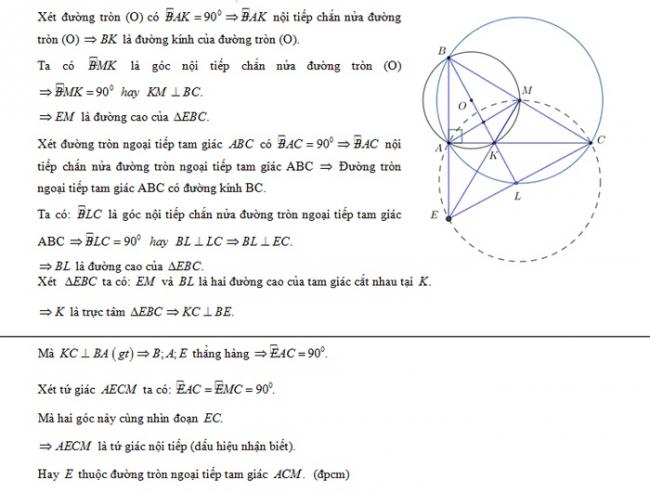
Cho tam giác ABC vuông tại A
Câu 6. (2 điểm)
Các số nguyên dương từ 1 đến 2018 được tô màu theo quy tắc sau: Các số mà khi chia cho 24 dư 17 được tô màu xanh; Các số mà khi chia cho 40 dư 7 - được tô màu đỏ. Các số còn lại được tô màu vàng.
a) Chứng tỏ rằng không có số nào được tô cả hai màu xanh và đỏ. Hỏi bao nhiêu số được tô màu vàng?
b) Có bao nhiêu cặp số \((a,b)\) sao cho \(a\) được tô màu xanh, \(b\) được tô màu đỏ và |\(a-b\)| bằng 2 ?
HẾT.
Đáp Án:
Câu 1:
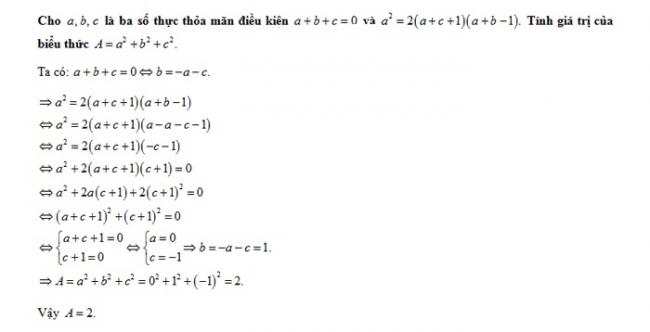
Câu 2:

Câu 3:

Câu 4:

Câu 5:
Câu 6:

Nếu không hiển thị đầy đủ đáp án, bạn hãy click vào link dưới đây:
https://doctailieu.com/dap-an-de-thi-tuyen-sinh-vao-10-toan-chuyen-tp-hcm-2018
